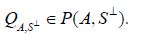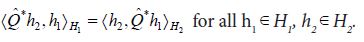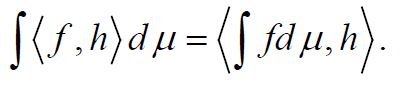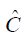Conditioning Gaussian Measure on Hilbert Space
For a Gaussian measure on a separable Hilbert space with covariance operator C, we show that the family of conditional measures associated with conditioning on a closed subspace S⊥ are Gaussian with covariance operator the short S(C) of the operator C to S. Although the shorted operator is a well-known generalization of the Schur complement, this fundamental generalization to infinite dimensions of the well-known relationship between the Schur complement and the covariance operator of the conditioned Gaussian measure is new. Moreover, the conditioning of infinite dimensional Gaussian measures appears in many fields so that this simply expressed result appears to unify and simplify these efforts.
We provide two proofs. The first uses the theory of Gaussian Hilbert spaces and a characterization of the shorted operator by Andersen and Trapp. The second uses recent developments by Corach, Maestripieri and Stojanoff on the relationship between the shorted operator and C-symmetric projections onto S⊥. To obtain the assertion when such projections do not exist, we develop an approximation result for the shorted operator by showing, for any positive operator A, how to construct a sequence of approximating operators An which possess An-symmetric oblique projections onto S⊥ such that the sequence of shorted operators S(An) converges to S(A) in the weak operator topology. This result combined with the martingale convergence of random variables associated with the corresponding approximations Cn establishes the main assertion in general. Moreover, it in turn strengthens the approximation theorem for shorted operator when the operator is trace class; then the sequence of shorted operators S(An) converges to S(A) in trace norm.
Keywords:Conditioning; Gaussian Measure; Hilbert Space; Shorted Operator; Schur; Oblique Projection; Infinite Dimensions
AMS subject classifications:60B05, 65D15
For a Gaussian measure μ with injective covariance operator C on a direct sum of finite dimensional Hilbert spaces 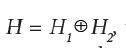
The primary purpose of this paper is to demonstrate that, for a Gaussian measure with covariance operator C, the covariance operator of the Gaussian measure obtained by conditioning on a subspace is the short of C to the orthogonal complement of that subspace. We provide two distinct proofs. The first uses the theory of Gaussian Hilbert spaces and a characterization of the shorted operator by Andersen and Trapp. The second proof, corresponding to the secondary purpose of this paper, uses recent developments by Corach, Maestripieri and Stojanoff on the relationship between the shorted operator and A-symmetric oblique projections. This latter approach has the advantage that it facilitates a general approximation technique that not only can be used to approximate the covariance operator but the conditional expectation operator. This is accomplished through the development of an approximation theory for the shorted operator in terms of oblique projections followed by an application of the martingale convergence theorem. Although the proofs are not fundamentally difficult, the result (which appears to have been missed in the literature) provides a simple characterization of the conditional measure, leading to significant approximation results. For instance, the attainment of the main result through the martingale approach feeds back a strengthening of the approximation theorem for the shorted operator that was developed for that purpose: when the operator is trace class the approximation improves from weak convergence to convergence in trace norm.
Conditioning Gaussian measures has applications in Information-Based Complexity and, beginning with Poincare, publications by e.g. Diaconis, Sul’din, Larkin, Sard, Kimeldorf and Wahba, Shaw, and Hagan they have been useful in the development of statistical approaches to numerical analysis [10-18]. Although they received little attention in the past, the possibilities offered by combining numerical uncertainties/errors with model uncertainties/errors are stimulating the reemergence of such methods and, as discussed in Briol et al. and Owhadi and Scovel, the process of conditioning on closed subspaces is of direct interest to the reemerging field of Probabilistic Numerics where solutions of PDEs and ODEs are randomized and numerical errors are interpreted in a Bayesian framework as posterior distributions [19-31] Furthermore, as shown in Gaussian measures are a class of optimal measures for minmax recovery problems emerging in Numerical Analysis (when quadratic norms are used to define relative errors) and conditioning such measures on finite-dimensional linear projections lead to the identification of scalable algorithms for a wide range of operators[20,32]. Representing the process of conditioning Gaussian measures on closed (possibility infinite dimensional) subspaces via converging sequences of shorted operators, could be used as a tool for reducing/compressing infinite-dimensional operators and identifying reduced models. In particular, it is shown in that the underlying connection with Schur complements can be exploited to invert and compress dense kernel matrices appearing in Machine Learning and Probabilistic Numerics in near linear complexity, thereby opening the complexity bottleneck of kernel methods [31].
Let us review the basic results on Gaussian measures on Hilbert space. A measure μ on a Hilbert space H is said to be Gaussian if, for each h
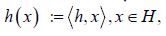
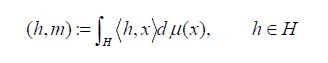
and its covariance operator C : H →H is defined by
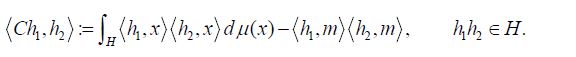
A Gaussian measure has a well defined mean and a continuous covariance operator, see e.g. Da Prato and Zabczyk [33]. Mourier’s Theorem, see Vakhania, Tarieladze and Chobanyan, asserts, for any m
Since separable Hilbert spaces are Polish, it follows from the product space version, see e.g. Dudley, of the theorem on the existence and uniqueness of regular conditional probabilities on Polish spaces, that any Gaussian measure μ on a direct sum 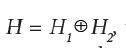


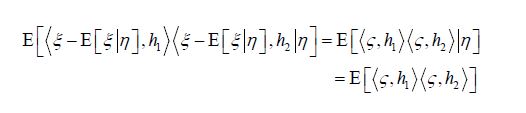
and so we conclude that, just as in the finite dimensional case, the conditional covariance operators are independent of the values of the conditioning variables [36].
Since both proof techniques will utilize the characterization of conditional expectation as orthogonal projection, we introduce these notions now. Consider the Lebesgue Bochner space L2 (H,μ,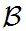 (H)) space of (equivalence classes) of H-valued Borel measurable functions on H whose squared norm
(H)) space of (equivalence classes) of H-valued Borel measurable functions on H whose squared norm
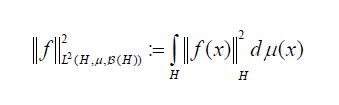
is integrable. For a sub σ-algebra 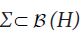
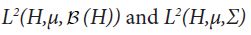
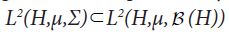
A symmetric operator A: H →H is called positive if(Ax,x)≥0 for all x∈H. We denote by L+(H) the set of positive operators and we denote such positivity by A≥0. Positivity induces the (Loewner) partial order ≥ on L+(H). For a closed subspace S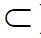

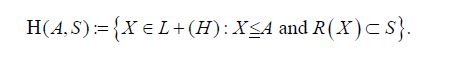
Then Krein and later Anderson and Trapp showed that H(A,S) contains a maximal element, which we denote by S(A) and call the short of A to S. For another closed subspace T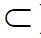
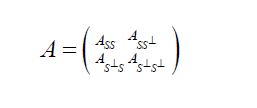
that is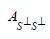
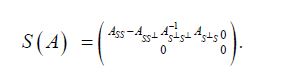
It is easy to show that the assertion holds under the weaker assumption that 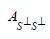

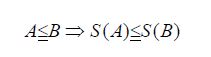
that is, S is monotone in the Loewner ordering, and for two closed subspaces S and T, we have
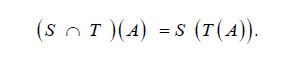
Finally, Theorem 6 of Anderson and Trapp asserts that if A: H →H is a positive operator and S⊂H is a closed linear subspace, then
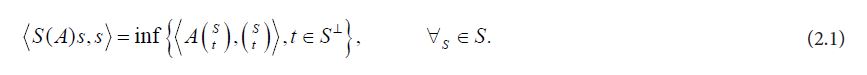
In Section 4.1 we demonstrate how the characterization (2.1) of the shorted operator combined with the theory of Gaussian Hilbert spaces provides a natural proof of our main result, the following theorem. Here we consider direct sum split 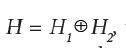
Theorem 2.1. Consider a Gaussian measure μ on an orthogonal direct sum 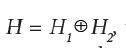

In this section, we will prepare for an alternative proof of Theorem 2.1 using oblique projections along with the development of approximations of the covariance operator and the conditional expectation operator generated by natural sequences of oblique projections. To that end, let us introduce some notations. For a separable Hilbert space H, we denote the usual, or strong, convergence of sequences by hn →h and the weak convergence byhnω→Let L(H) denote the Banach algebra of bounded linear operators on H. For an operator A
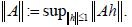


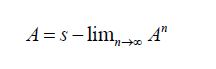
if Anh→Ah for all h∈ H, and we say that An →A weakly or
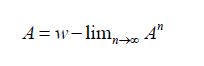
if 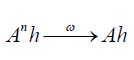


is finite for some orthonormal basis, where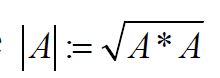
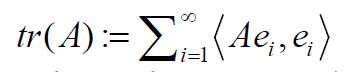
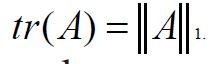
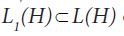
increases from left to right in strength.
For a positive operator A: H →H, let us define the set of (A-symmetric) oblique projections
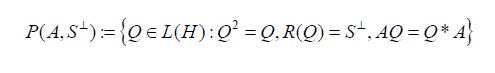
onto S⊥, where Q* is the adjoint of Q with respect to the scalar product<·,·>on H. The pair (A, S⊥) is said to be compatible, or S⊥ is said to be compatible with A, if P(A, S⊥) is nonempty. For any oblique projection Q

Moreover,when (A,S⊥) is compatible, according to Corach, Maestripieri and Stojanoff,there is a special element 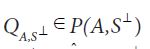
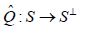
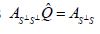
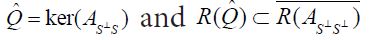

their Theorem 3.5 asserts that
When the pair (A,S⊥) is not compatible, we seek an approximating sequence An to A which is compatible with S⊥, such that the limit of S(An) is S(A). Although Anderson and Trapp show that if An is a monotone decreasing sequence of positive operators which converge strongly to A, that the decreasing sequence of positive operators S(An) strongly converges to S(A), the approximation from above by An:=A+1/nI determines operators which are not trace class, so is not useful for the approximation problem for the covariance operators for Gaussian measures. Since the trace class operators are well approximated from below by finite rank operators one might hope to approximate A by an increasing sequence of finite rank operators. However, it is easy to see that, in general, the same convergence result does not hold for increasing sequences. The following theorem demonstrates, for any positive operator A, how to produce a sequence of positive operators An which are compatible with S⊥ such that S(An) weakly converges to S(A)[2,38].
Henceforth we consider a direct sum split 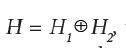
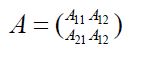
where the components are defined by Aij:=AΠ*i,i,j=1,2.
Theorem 3.1. Consider a positive operator A: H →H on a separable Hilbert space. Then for any orthogonal split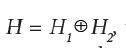
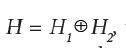
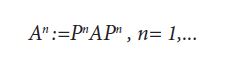
is compatible with H2 and
Remark 3.2. For an increasing sequence An of positive operators converging strongly to A, the monotonicity of the shorting operation implies that the sequence H1(An) is increasing, and therefore Vigier’s Theorem implies that the sequence H1(An) converges strongly. Although the sequence An:=PnAPn defined in Theorem 3.1 is positive and converges strongly to A, in general, it is not increasing in the Loewner order, so that Vigier’s Theorem does not apply, possibly suggesting why we only obtain convergence in the weak operator topology. With stronger assumptions on the operator A and a well chosen selection of an ordered orthonormal basis of H2, we conjecture that convergence in a stronger topology may be available. In particular, as a corollary to our main result, when A is trace class, we establish in Corollary 3.4 that
H1(An)→H1(A) in trace norm.
For any m
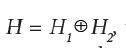
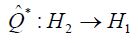
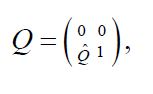
and denote by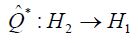
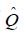
The following theorem constitutes an expansion of our main result, Theorem 2.1, to include natural approximations for the conditional covariance operator and the conditional expectation operator.
Theorem 3.3. Consider a Gaussian measure μ on an orthogonal direct sum 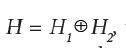

If the covariance operator C is compatible with H2, then for any oblique projection Q in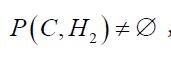
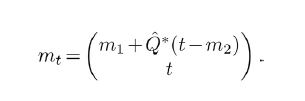
In the general case, for any ordered orthonormal basis for H2, let H2n denote the span of the first n basis elements, let p p p denote the orthogonal projection onto 

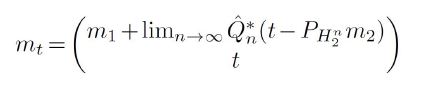
for μ-almost every t. If the sequence Qn eventually becomes the special element Qn=QCn,H2 defined near (3.2), then we have
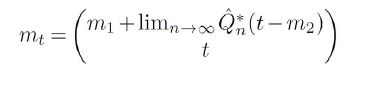
for μ-almost every t.
As a corollary to Theorem 3.3, we obtain a strengthening of the assertion of Theorem 3.1 when the operator A is trace class.
Corollary 3.4. Consider the situation of Theorem 3.1 with A trace class.Then
H1(An )→H1(A) in trace norm
First proof of Theorem 2.1 Consider the Lebesgue-Bochner space 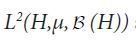
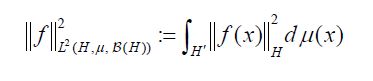
is integrable. For any square Bochner integrable function 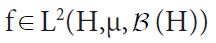

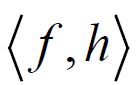
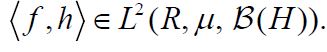

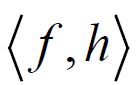
Now consider the orthogonal decomposition 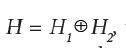
 (H2). Let us denote the shorthand notation
(H2). Let us denote the shorthand notation
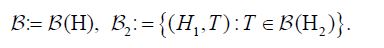
The definition of conditional expectation in Lebesgue-Bochner space, that is that 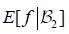
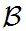 2-measurable function such that
2-measurable function such that
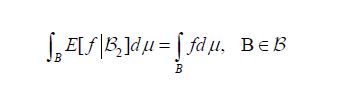
combined with Hille’s theorem [13,Thm. II.6], that for each h
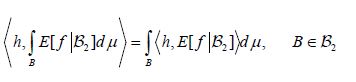
and
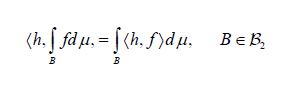
implies that
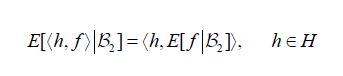
thus implying the following commutative diagram for all h
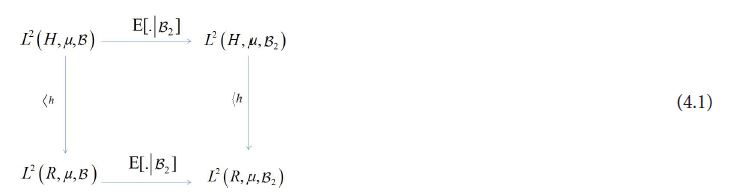
When μ is a Gaussian measure, the theory of Gaussian Hilbert spaces, see e.g. Jansen, provides a stronger characterization of conditional expectation of the canonical random variable X(h):=h,h

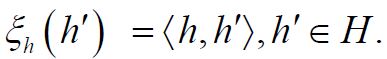


 ), for all h
), for all h
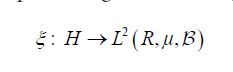
denote the resulting linear mapping defined by
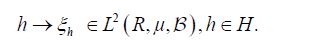
It is straightforward to show that ξ is injective if and only if the covariance operator C of the Gaussian measure μ is injective. By the definition of a centered Gaussian vector X, it follows that the law (ξh)*μ in R is a univariate centered Gaussian measure, that is ξh is a centered Gaussian real-valued random variable. Consequently, let us consider the closed linear subspace
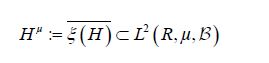
generated by the elements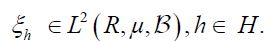
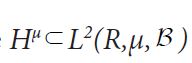
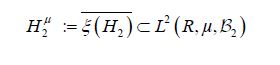
generated by the elements 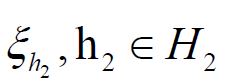
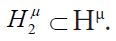

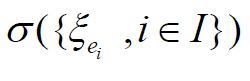

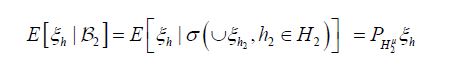
where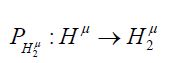
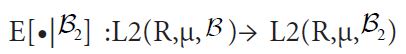
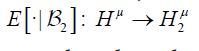
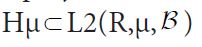
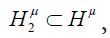
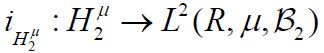
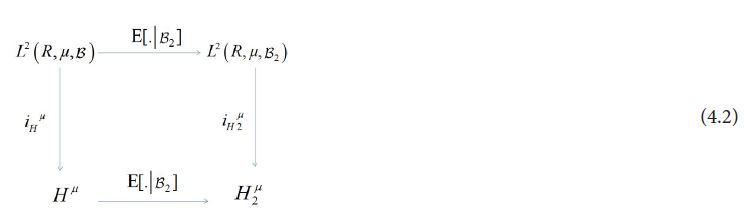
which when combined with Figure 4.1, representing the commutativity of vector projection and conditional expectation, produce the following commutative diagram for all h

Although there is a natural projection map PH2:H→H2 for the bottom of this diagram, in general it cannot be inserted here and maintain the commutativity of the diagram. This comes from the fact that there may exist an h
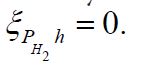
We are now prepared to obtain the main assertion. The covariance operator of the random variable X is defined by
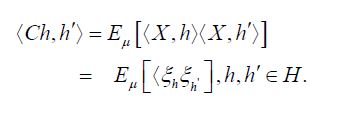
Moreover, by the theorem of normal correlation and the commutativity of the diagram (4.1), the conditional covariance operator is defined by
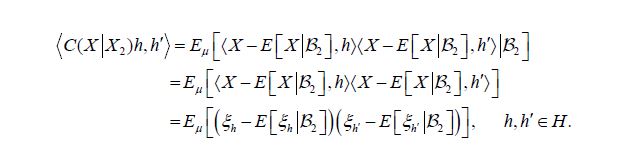
In terms of the Gaussian Hilbert spaces 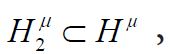

and
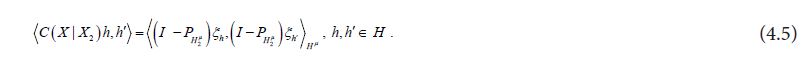
Since the orthogonal projection pHμ2 is a metric projection of Hμonto,Hμ2 we can express the dual optimization problem to the metric projection as follows: for any h


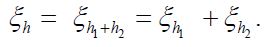
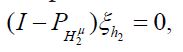
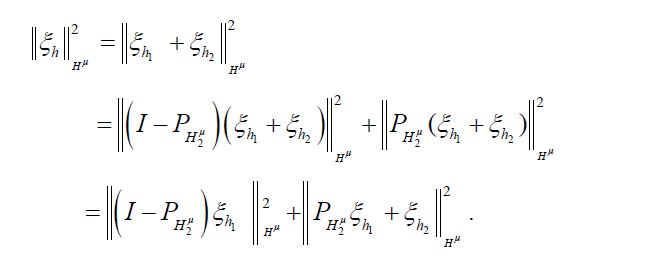
Since in the second term on the right-hand side 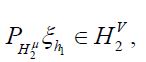
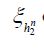
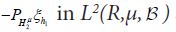
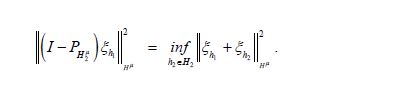
From the identifications (4.4) and (4.5), we conclude that
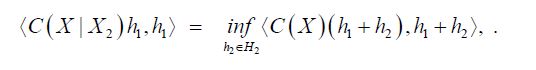
Therefore, Anderson and Trapp implies the assertion
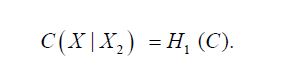
The assertion in the non-centered case follows by simple translation.
Proof of Theorem 3.1 Since 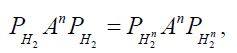
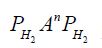

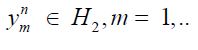
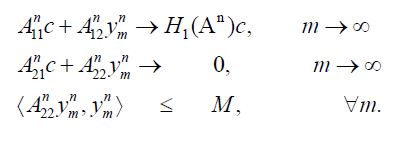
Since 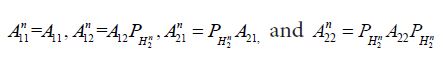
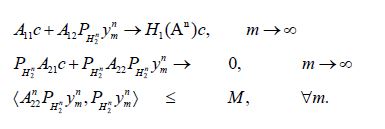
Since these equations only depend on 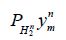
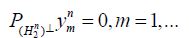
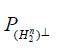
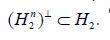
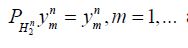
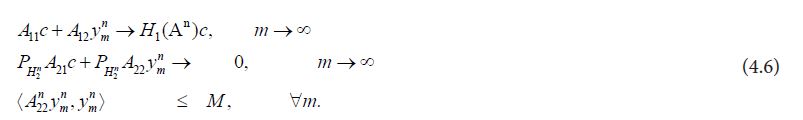
It follows from 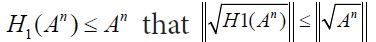
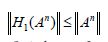
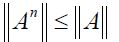
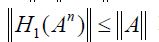
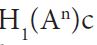

for some d' depending on the subsequence. Now the strong convergence of the lefthand side to the righthand side in (4.6) is maintained for the subsequence n' and, since for the subsequence the first term on the righthand side converges weakly to d′, it follows that we can define a monotonically increasing function m(n') and use it to define a new sequence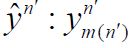
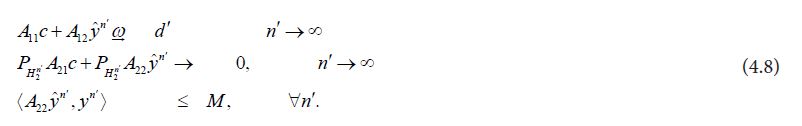
Since 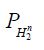
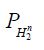
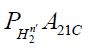
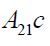
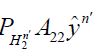

for all n',so that the sequence 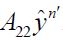
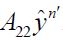

From Kakutani’s generalization of the Banach-Saks Theorem it follows that we can select a subsequence `n of n′ such that the Cesaro means of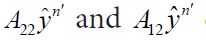
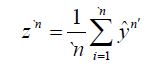
we have
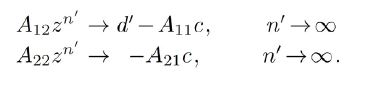
Since A22≥0 it follows that the function 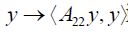
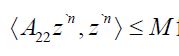
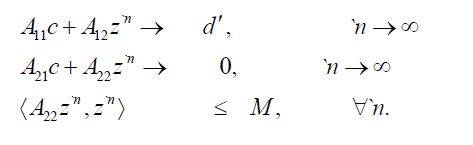
It therefore follows from Theorem 1 of Butler and Morley that
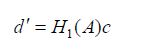
Consequently, by (4.7), we obtain that

Since this limit is independent of the chosen weakly converging subsequence, it follows that the full sequence weakly converges to the same limit, that is we have

and since c was arbitrary we conclude that
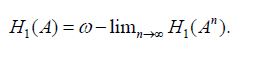
Proof of Theorem 3.3 Let us first establish the assertion when C is compatible with H2. Consider the operator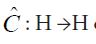

Since C is compatible with H2, there exists an oblique projection Q

Since Q*C =CQ it follows that E*C =CE, and since Q is a projection, it follows that QE =EQ= 0 and that E is a projection. Moreover, since R(Q) = H2 it follows that ker(E) = H2, so that we obtain P2Q=Q and EP1 =E and therefore Q*P2 =Q* and P1E* =E* . Consequently, we obtain
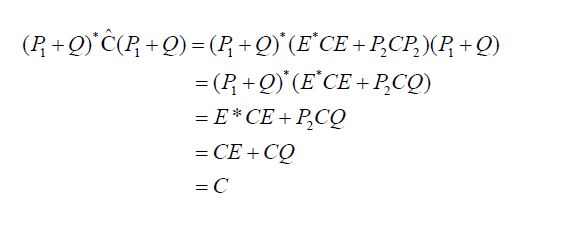

Since Q is a projection onto H2, it follows that P1+Q is lower triangular in its partitioned representation and therefore the fundamental pivot produces an explicit, and most importantly continuous, inverse. Indeed, if we use the partition representation
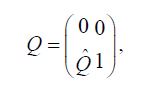
we see that
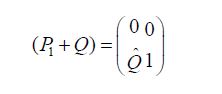
from which we conclude that
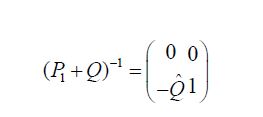
Without partitioning, using P1Q= 0 and QP2 =P2, we obtain
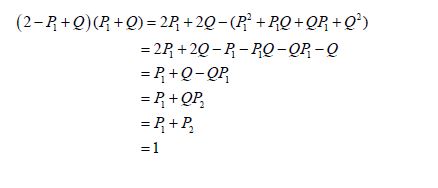
and so confirm that

Following the proof of Lemma 4.3 of Hairer, Stuart, Voss, and Wiber, let N (m,C) denote the Gaussian measure with mean m and covariance operator C and consider the transformation
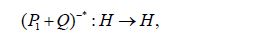
where we use the notation A−* for (A−1 )* = (A*)−1 . From (4.14) we obtain

so that the transformation law for Gaussian measures, see Lemma 1.2.7 of Maniglia and Rhandi, implies that
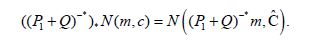
Since
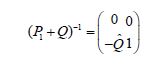
we obtain
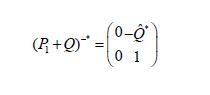
and therefore
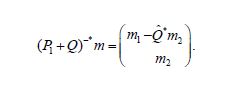
Since the partition representation of
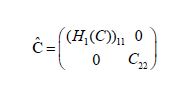
the components of the corresponding Gaussian random variable are uncorrelated and therefore independent. That is, we have
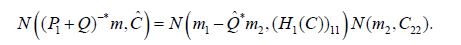
This independence facilitates the computation of the conditional measure as follows. Let X = (X1,X2) denote the random variable associated with the Gaussian measure N (m,C) and consider the transformed random variable Y = (P1+Q)−*X with the product law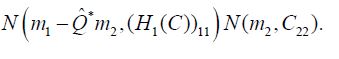
then,
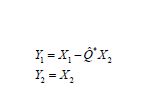
can be used to compute the conditional expectation as
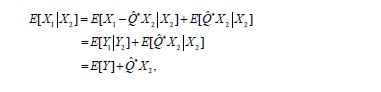
obtaining

so that we conclude that
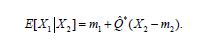
A similar calculation obtains the covariance

thus establishing the assertion in the compatible case.
For the general case, we do not assume that C is compatible with H2. Consider an ordered orthonormal basis for H2, let H2n denote the span of the first n basis elements, let 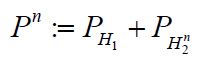
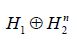
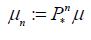
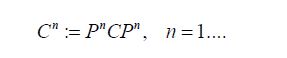
As asserted in Theorem 3.1, Cn is compatible with H2 for all n, and the sequence H1(Cn) converges weakly to H1(C). Let c(X1|H2n) and C(X1|X2) denote the conditional covariance operators associated with the measure μ. Then we will show that c(X1|H2n)=H1(cn)so that the assertion regarding the conditional covariance operators is established if we demonstrate that the sequence of conditional covariance operators c(X1|H2n) converges weakly to C(X1|X2).
To both ends, consider the Lebesgue-Bochner space L2(H,μ,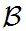 ) space of (equivalence classes) of H-valued Borel measurable functions on H whose squared norm
) space of (equivalence classes) of H-valued Borel measurable functions on H whose squared norm
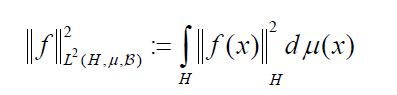
is integrable. Since Fernique’s Theorem, implies that the random variable X is square Bochner integrable, it follows that the Gaussian random variables PnX are also square Bochner integrable with respect to μ. Let us denote 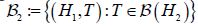
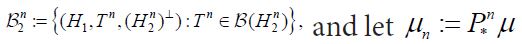
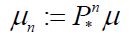
Now consider a function f: H →H which is Bochner square integrable with respect to μ and satisfies f oPn =f. Then, using the change of variables formula for Bochner integrals, see Theorem 2 of Bashirov, et al. along with the fact that 
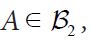
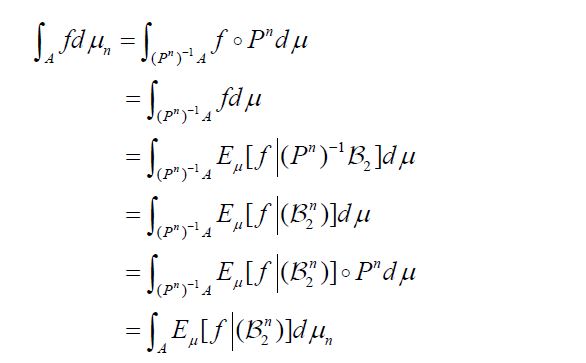
we obtain

and conclude that the sequence 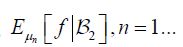
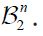

is a martingale. Since conditional expectation is a contraction, it follows that the L2 norm of all the conditional expectations are uniformly bounded by the L2 norm of X. Then by the Martingale Convergence Theorem, Corollary V.2.2 of Diestel and Uhl, 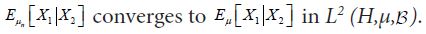

for all n, so that for h1,h2 
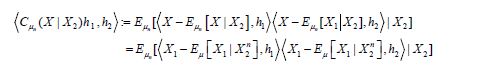
and since the integrand 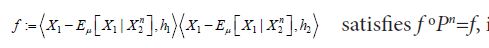
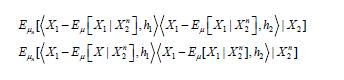
so that using the theorem of normal correlation, we obtain
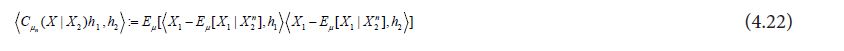
Since the theorem of normal correlation also shows that
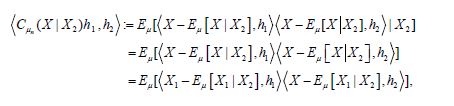
the difference in the covariances can be decomposed as
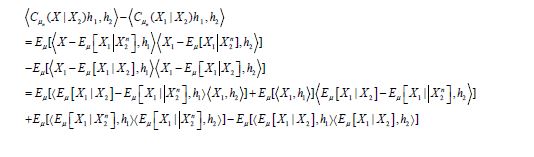
where the last term can be decomposed as
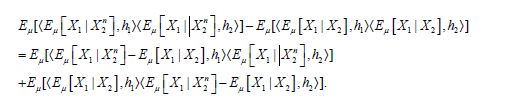
Then since conditional expectation is a contraction on L2(H,μ,
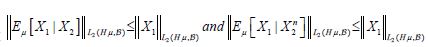
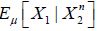
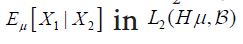
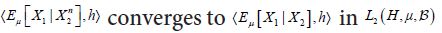

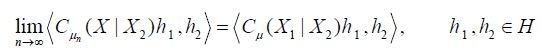
so that we obtain
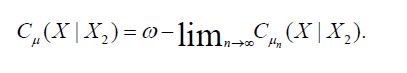
Since Cn is compatible with H2 for all n, and the compatible case demonstrated in (4.18) that

for all n, and Theorem 3.1 asserts that
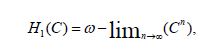
we conclude that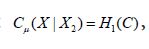
For the means, observe that since μ is a probability measure, it follows that X and therefore X1lie in the Lebesgue-Bochner space L1(H,μ,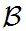 ), and since by Diestel and Uhl the conditional expectation operators are also contractions on L1(H,μ,
), and since by Diestel and Uhl the conditional expectation operators are also contractions on L1(H,μ,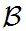 ) it also follows that
) it also follows that 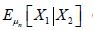
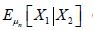
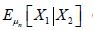

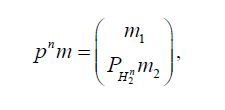
is the mean of the measure μn, the assertion in the compatible case demonstrated that the conditional means
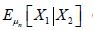

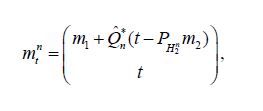
Since the conditional means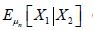
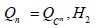
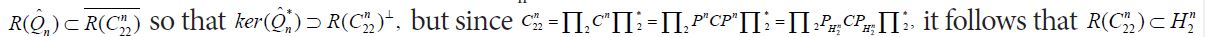
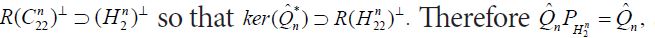
Proof of Corollary 3.4 By Mourier’s Theorem, there exists a Gaussian measure μ on H with mean 0 and covariance operator C :=A. Looking at the end of the proof of Theorem 3.3, since conditional expectation is a contraction on L2(H,μ, ) it follows that
) it follows that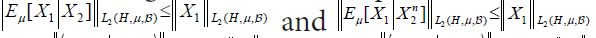

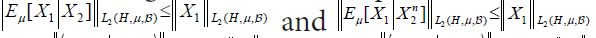

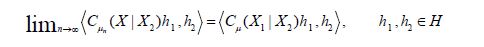
Uniformly for 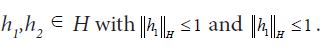
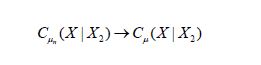
in the uniform operator topology.
According to Maniglia and Rhandi or Da Prato and Zabczyk, for a Gaussian measure μ with mean 0 and covariance operator C, we have
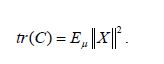
From (4.22), by shifting to the center, we obtain that
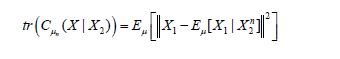
And
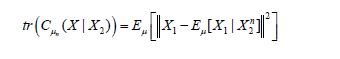
and therefore the difference
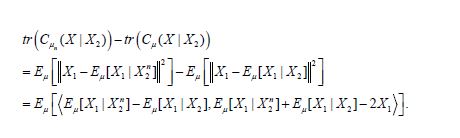
Therefore, the Cauchy-Schwartz inequality, the L2 convergence of Eμ[X1|X2n] to Eμ[X1|X2], and the uniform L2 boundedness of Eμ[X1|X2n] Eμ[X1|X2] and X1, implies that
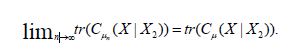
Since 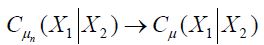
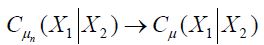
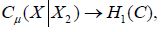
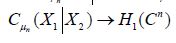
The authors gratefully acknowledge this work supported by the Air Force Office of Scientific Research under Award Number FA9550-12-1-0389 (Scientific Computation of Optimal Statistical Estimators).