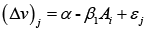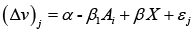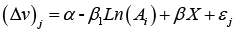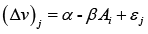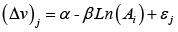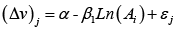Determination of the Availability of Payment for Conservation and Improvement Activities of Wetlands Ecosystem of the Huaraz City, Peru
Contingent Valuation Method (CVM) was used with the purpose of determining the willingness to pay (WTP) of the citizens of Huaraz city – Peru (Ancash Region) in order to estimate a financial fund to subsidize the design and implementation of conservation and restoration activities of the wetland ecosystem. To estimate the WTP, a LOGIT probabilistic model was used; which is based on the theoretical proposal of Bishop-Heberlein. Results indicate that the most influential variables in the WTP, are a set of variables of “appreciation” (of the citizen’s) regarding the ecological importance of the wetlands in their region. However, socioeconomic variables, such as income, age, education, etc., were not significant in explaining the WTP variation. The best statistical indicator for measuring the WTP was the median, which was estimated at $1.05 USD/family/month, revealing that in Ancash region (Peru) it could raise annually by an estimated of $312,266 USD. An important conclusion is that economic valuation is key to design and implement activities of conservation and improvement of the wetlands, this being the beginning of a process that will end successfully if some remaining steps are completed.
Keywords: Wetlands Ecosystem; Willingness to Pay; LOGIT Model
Huaraz city is located in north-central Peru, about 420 km north of Lima, and is situated at an altitude of 3,052 metres (10,013 ft); it is the capital city of the Ancash Region and has the largest population center in the agriculturally important “Callejón de Huaylas” valley. The “Callejón” (in Spanish roughly meaning large valley or corridor) is a north-south valley bounded on the east by the Cordillera Blanca (permanent snow lines and glaciers) and on the west by the Cordillera Negra (no snow lines or glaciers, hence black). The Cordillera Blanca includes Huascaran, the highest mountain in Peru at 6,768 metres (22,205 ft) and the third highest in the Western Hemisphere. In fair weather, Huascaran and the adjacent peak Huandoy are clearly visible from Huaraz. As of July 2012, the metropolitan area of Huaraz had 117,774 inhabitants; in 2015 it has been estimated at 157,000 [1].
Wetlands ecosystems are natural mattresses formed over thousands of years around Huaraz; that hold large amounts of water and are located in the mountains near the snow lines, lagoons, rivers and streams that supply water to Huaraz. Around the city, there are five rivers: Llaca, Cojup, Quilcayhuanca, Shallap, and Rajucolta (MINAM, 2014), which mainly feed on glacial meltwater from the Cordillera Blanca, the remainder coming from rainwater and surface/subsurface waters. These rivers form the structural base of the wetlands, which are located along the riverbanks, attenuating the effects of large avenues. The wetlands have the same name as the rivers [2]. These ecosystems constitute one of the most important natural resources in terms of water storage and regulation (ecosystem service), reduction of damage caused by mudslides and floods, purifying polluted water from snowfalls in the process of climate change, and provide beautiful landscapes with abundant flora and fauna for recreation and tourism.
Around Huaraz the structure and function of wetlands is being significantly affected by the impacts derived from the mismanagement, overgrazing, deforestation, drainage, changes in land use and also climate change, which interact with each other to determine their ecological status. Due to lack of technical knowledge, and in an attempt to improve their income, the local population presses on the wetlands, finally altering its capacity to provide ecosystem services that are critical for the Huaraz city (supply and regulation of water supply, among others).
In this ecological and social context, the development of Sustainable Economic Activities (SEA) is important for the region, since it would allow to state socio-economic development alternatives against the overuse of wetland ecosystems. SEA is a tool to promote execution of projects that allow implementation of environmentally sustainable economic activities, such as fish farming, livestock, tourism, among others. A good reason to finance SEA projects is to raise awareness to Huaraz citizens about the wetland importance; also valuing their willingness to pay (WTP) for the design and environmental services provided by this type of ecosystem.
WTP is usually obtained by using economic valuation methods. The Contingent Valuation Method (CVM) is the most widely used for valuation of ecosystem services, it uses as practical tool a probabilistic econometric model that simulates a hypothetical services market, from which economic values are estimated for improvement of the service. CVM surveys a target group of potential supporters for the ecosystem service involved. In this study, contingent valuation method has been used in order to determine the WTP for the design and implementation of a conservation program for wetlands ecosystem environment in Huaraz city, Peru. This document has five sections, including this introduction; the rest of the sections present a brief theoretical framework, methodology, results and main conclusions.
In any economy there are a large number of environmental goods and services that do not necessarily operate in a conventional market in which the respective prices could be generated and automatically discovered; however, prices need economic valuation in order to have an indicator of social welfare, which allows public policy decision-making, among others [3]. The final purpose of environmental economic valuation is to obtain information and facilitate decision making in areas such as regulation and environmental management; In other words, guiding the use of resources in activities that report net social gains. Results of the economic valuation are useful in the design and application of public policy, such as cases of tax policy, subsidies, conservation or regulatory restrictions, etc [4].
Methods for economic valuation of ecosystem services (such as those provided by water resources) are diverse, and start from theoretical concepts of estimating surpluses of consumers and producers [5]. One of the most widely used methods is “Contingent Valuation” (CVM), which is the most appropriate method to measure values of changes for improvement of existing ecosystem services. The CVM allows simulating a hypothetical market for goods and services with no fixed prices in a real market, by surveying a target group of potential supporters for a certain environmental good or service. Each respondent of the target group is asked for their maximum willingness to pay (WTP) for an improvement in the quality and quantity of the environmental good or service. In this way, the value (of the good or service) is estimated for the average consumer of the target group [6].
Practical application of the CVM is carried out by means of econometric estimations that allow estimating the welfare measures of people demanding an ecosystem service; such parametric estimates are mostly the mean and median of the WTP, obtained from regression models that explain the determinants of the individuals WTP. The regression model is based on functional forms of economic utility, such as those proposed by Hanemann (1984) and Bishop-Heberlein (1979), which are alternative ways of estimating the WTP [7-9].
Estimation of the economic value of an ecosystem service has its practical expression in certain indicators or social welfare measures. It also has theoretical support in functions of economic utility, which in practical terms will depend on the income or available income (y) and prices to which the different services must be acquired (p). Therefore, the utility function of individuals can be expressed as:
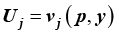
Where:
vj = indirect utility function
j = 0, 1 in an initial and another modified situation, respectively
P = vector of price of ecosystem good or service
y = family income
Since not all goods or services have observable prices in the market (which is precisely the case of environmental goods and services), then it is possible to write equation (1) more generally as the following one [9]:
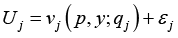
Where:
vj = indirect utility function
P = vector of price of the good or service; obtained from asking the question “would you be willing to pay a bid (S/.Ai) to make an
improvement in the environmental service”?
qj= environmental quality related to utility of individuals. The variable can be generalized to include socio-economic characteristics of relevant individuals [9].
εj = Random component that may incorporate unknown elements.
In this case, equation (2) expresses the situation of individuals against to the option of an improvement in environmental quality, going from q0 to q1, for which they must pay a certain bid Ai (the subindex i indicates the specific amount that is bidden and that is part of the payment vector). The answer is designed as a dichotomous variable (yes/no).
The probability of an affirmative answer (by the respondent) will be the probability that its true WTP (C) be greater than or equal to the amount being bidden [10]. That is to say:
Where:
C = represents the true WTP of each individual
Ai = Optimal vector of payments (bids o tariffs) that includes the set of rates to which the interviewees are asked about their WTP.
Incorporating equation (3) into (2), we can get the expression that the respondent is willing to pay the amount Ai:
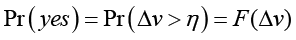
Where F is the cumulative distribution function of η and η = (ε0-ε1)
Δv is the change in utility between an initial situation and a modified situation (0, 1, respectively).
Equation (4) represents an indirect utility function. By choosing a probabilistic distribution for η and giving a functional form to the indirect utility function, it is possible to obtain the parameters of such equation, using information provided by binary answers (yes/no) to the dependent variable. For this purpose, a logistic distribution function can be used (LOGIT), among others.
Based on equation (4), Hanemann (1984) has proposed a linear indirect specific utility equation, such as [7]:
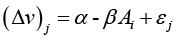
In (5) we expect - as a key hypothesis - an inverse relationship between Ai(the bid associated with the WTP), and the change in utility Δv (operationally represented by the probability of a dichotomous bid response Ai).
Alternatively, Bishop-Heberlein (1979) has suggested the use of the following nonlinear function [8]:
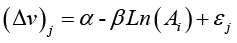
Such a functional form does not necessarily require the assumption of symmetry of the distribution of errors. For more details see Vásquez, et al. [9].
Estimation of the abovementioned indirect utility models (5) and (6), requires the use of an econometric model of the so-called probabilistic econometric models, whose distinctive characteristic is the presence of a discrete dependent variable (dichotomous or polyatomic), which depends on a set of determining factors (Ai, among others). Regression analysis is commonly used to obtain estimation of the probability of “success” of a given event (in this case the success that individuals pay the bid Ai).
The most commonly used type of econometric model is the LOGIT model, which could express the probability of payment of the indicated bid (Ai) as follows [11]:
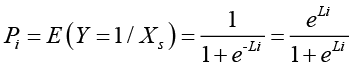
Where
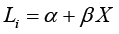
X is a matrix containing the bid associated with the WTP (Aio LnAi), and which can be expanded to include a set of additional regressors (environmental or socioeconomic variables).
In the context of economic valuation of an ecosystem service, Pi represents the probability that an individual pays the bid randomly indicated in the interview; Li would represent the change of utility (Δv) of equations (5) and (6).
It is demonstrable to determine an operative LOGIT equation as follows:
Equation (8) is actually a semi-logarithmic functional expression, whose estimated parameters represent semi-elasticities. In the present study, the term (α+βX) changes according to the specific formulation, that being either the Hanemann linear proposal or the Bishop-Heberlein logarithmic proposal. The estimation method is Maximum Likelihood (ML), with parameters αβy estimated using assumptions about the error distribution: logistic distribution in this case1 (Gujarati and Porter, 2010, appendix of chapter 15) [12].
Welfare measures are finally the central purpose of the economic valuation effort, since they are individual quantitative representation of the value of the assessed environmental goods or services. In general, the welfare measures considered important in this document, are the average and median of the WTP, and can be obtained from the own estimation results of the used probabilistic model (LOGIT in this case) [13].
The Contingent Valuation Method (CVM) with the use of an operating equation LOGIT has been used in this study to estimate the economic value of the wetlands Ecosystem of the Environment of Huaraz city, Peru. The CVM is sustained, from the practical point of view, in obtaining primary source data that feed the probabilistic model with the purpose of estimating welfare measures that finally allow obtain the economic value of the ecosystem service. In the following subsections the practical procedures of the above are detailed.
Data was obtained from a random sample, of probabilistic nature (n), which is made viable through application of a survey to a target group of potential users of a specific good or environmental service. Specifically in this case, a representative sample size was obtained, using a probabilistic sampling method that finally allowed inferring the results to the total population: the simple random sampling method, considering the following formula:
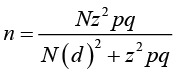
Where:
N= Total population size
z = 1.96 (level of significance, based on 95% confidence estimation)
pq= Is an estimated assumption of the dichotomous WTP variance, based on a binomial probability distribution (0.5 * 0.5). It is
assumed that half of the population would accept to pay the proposed bid and the other half would reject the payment.
d = Margin of the WTP estimation interval, for a total of 10% margin.
The total estimated sample size was 270; the interview was applied to citizens of Huaraz capital city (population of 24,783, according to INEI statistics, 2012) [14].
Kong, et al. indicates that the best way to estimate the willingness to pay (WTP) for conservation or improvement of a natural resource, is a “face to face” interview, applied to a representative sample of the population surrounding the target area [15]. In addition, Riera, et al. recommend that two surveys should be used, one “open” survey as a pilot study to determine the payment vectors; and another “closed” survey that contemplates a dichotomous question (acceptance or rejection) of the payment vector estimated in the previous survey and socioeconomic characteristics (Table 1) [6]. In the present study two types of survey were applied to the population, one of open format and another of closed format. The first was carried out as a pilot study, as previous stage or first stage, with the purpose and characteristics summarized in Table 1; the second survey was applied in the formal, definitive study.
1It is also possible to use a normal probabilistic distribution, which permit to use of a PROBIT or NORMIT model.
In this regard, structure of the closed survey was divided into three parts. The first one is related to perceptions of the people with respect to wetlands of the surroundings areas of Huaraz city. The second one is to know their willingness to pay for the improvement of the wetlands under study. The third part is about socioeconomic aspects of the interviewed people [10].
The idea of establishing the relation between the dichotomous dependent variable (yes/no and accepts the bid) and the tariff itself is to vary the latter and verify how the answers (yes/no) change precisely responding to changes in the rate. Optimal payment vector is a matrix containing an “optimal” set of bids that are correlated with the dichotomous variable that expresses the willingness to pay. Then, each sample unit (citizen interviewed) is presented with one of the rates (or “bid” of the payment vector) and is asked to be willing to pay the value of such fee. Previously, rates are estimated using the DWEABS method (“Distribution with Equal Area Bid Selection”), designed by Cooper (1993), and widely used in contingent valuation studies (Table 2) [3,16].
In this case, bids are distributed and applied in a random way, to observations that are part of the 271 surveys.
Utility functions suggested by Hanemann (1984) and Bishop-Heberlein (1979) become operative through the use of probabilistic models; parameters are estimated by an econometric model of this type [7,8]. According to the above specification of equation 9, the LOGIT model is one of the most used probabilistic models. In this study four equations were estimated to establish the determinants of the WTP, all based on functional forms suggested by Hanemann and Bishop-Heberlein. For each functional form, an equation with only the “induced” rate as a regressor variable (models 1 and 2) was specified and estimated, as well as another equation with the additional inclusion of a significant set of socioeconomic and environmental regression variables (models 3 And 4). Table 4 shows the types of four estimation models.
As average and median are the welfare measures most commonly used in contingent valuation, in this case these two statistical indicators were estimated, based on the results of the estimation of the four probabilistic models used. In the case of functional utility forms underlying the LOGIT model estimation, the Hanemann and Bishop-Heberlein proposals (equations 6 and 7 respectively), welfare measures were calculated according to formulas shown in Table 4 below.
To note that columns named “Average” and “Median”, the values of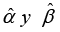 
are derived from estimation of the intercept term and marginal slope associated with the linear and logarithmic equations of the first column. WTP is estimated from use of such social welfare indicators in Table 4, which depend directly on the parameter estimation of the LOGIT model. Welfare measures are interpreted as maximum amount that the inhabitants of Huaraz city would be willing to pay for improvement to conserve the surrounding wetlands.
Results of Table 5 show that wetlands are important for the Huaraz population. Seventy percent of the respondents said they do family activities in their natural areas; also 54% said they know their wetlands and their importance for the region. Consistent with these findings, it was found that more than 80% of respondents had knowledge that the Ancash region wetlands are in danger, and therefore require protection. These results are consistent with what was stated by Riera, et al. (2005) and Villena, et al. (2013), with respect to the fact that the population assigns a greater value of importance when they are familiar with the resource under study [6,10].
However, it is important to highlight that 16% of the participants also indicated that they know little about the Program for Improvement and Conservation (PIC) of wetlands, and the concept of environmental service (only 22%). This is a similar result found in other studies in Peru [18].
In the present study, a pilot study with open format was applied to 200 people, from which we obtained the table frequencies of the low or upper limits, or WTP values, using an asymmetric base distribution for estimation of the optimal payment vector. Lognormal function was used to obtain the optimal payment vector presented in Table 2 above. It follows that in the final interview, there were up to 8 types of questionnaires that differed from each other exclusively in the amounts of simple dichotomous question of WTP (the DWEABS method was used to obtain optimal bids).
Out of 271 interviewees, only 32% were initially willing to collaborate with the project, according to the differential value initially asked. However, respondents who stated that they were not willing to pay the indicated initial bid, were asked the question of how much would be the maximum amount they could afford? In this second case, 27 of 185 interviewees - 14.6% reiterated that they were not willing to pay anything for the wetland conservation. Then, it became clear that, in total, 10% reiterated a zero WTP and 90% of respondents would pay a minimum amount of money to conserve the resource (Table 6). Similar results were found in the studies by Barrantes & Flores (2013) and Villena & Lafuente (2013), where only 25% of the inhabitants of Cerro de Pasco (Peru) and 31% among the inhabitants of the Tiataco community and the city of Cochabamba (Bolivia), respectively, were willing to pay the amount established for the improvement and conservation of the natural resource under study [10,18].
Also in Table 6 the negative relationship between the bid amount and the WTP can be clearly noticed. That is, the higher the bid rate, the lower the WTP, with “negativity” reaching a percentage of up to 88% when the asked bid had reached S/.18 soles. In contrast, for the case of the minimum rate (≤ 1), the negativity only reached 21%. In general, these results are consistent with others, such as Barrantes and Flores (2013), Riera, et al. (2005) and Yomary and Alvarez, in the sense that the larger the payment vector, the lower the willingness to pay for the surveyed people [3,6,18].
In addition, Table 7 shows that 35% of total 185 people (65 people) who refused to pay the initial bid, indicated that payment is “responsibility of the Government” (answers 4 and 6), disengaging their own responsibilities. Twenty-one percent said they did not have the means to pay. Other responses include the distrust in management of the fund and the responsibility of mining companies. It is important to note that only 4% indicated that the wetlands problem was not a priority.
It should be noted that these results (Table 7) are similar to those inferred from the study by Yomary and Alvarez (2013), in the sense that to improve the air quality of Rancagua city, Chile [3]. The indicators of negativity to the WTP payment show similar percentages, 32% mention that the local and national governments should be responsible for the financing of a certified institution. In addition, 24% of respondents do not have enough money to support this new body, 15% indicate that they must pay for those that cause the pollution and 5% indicate that this is not a priority issue for the population.
As aforementioned, four equations were estimated to establish the determinants of WTP, using a LOGIT econometric model. Table 8 shows results of alternative functional forms under LOGIT according to those shown in Table 3.
Note that models 1 and 2 consider the linear and logarithmic function of Hanemann and Bishop-Heberlein respectively; both explain the probability of success in payment, only as the function of the proposed bid. In both cases, negative coefficients (-0.199 in model 1 and -1.304 in model 2) express that reducing the bid, by a certain percentage, would increase the probability in favor of WTP (for conservation and improvement activities in the wetlands around Huaraz). According to the Akaike criterion, the “logarithmic” model 2 was the most appropriate, and it was then used for determination of welfare measures. Model 2 also had a better goodness of fit (according to coefficients R2 McFadden and R2 account).
A similar case is observed in the study by Villena and Lafuente (2013), where only the BID is considered a regressor in the distribution of models 1 and 2 to the surrounding population of the natural resource [10]. The BID coefficient of this study showed a negative sign for both models, -0.0448 and -2.6627, respectively. In addition, to this study, the measures of goodness of fit (R2 McFadden and Chi Square) and Akaike criteria are much better in model 2 than model 1.
Models 3 and 4 are an extension of models 1 and 2, since both include and show results related to influence of an additional set of regressor variables in both models (only the most relevant ones are shown in Table 8). In both models, 3 and 4, there was also a negative relationship between an increase in bids and the probability in favor of a positive WTP response; that is, WTP is also increased when the asked bid decreases (and vice versa). Barrantes and Flores (2013), used a LOGIT model and considered a wide range of study variables; found a BID coefficient of -0.1168 (P value <0.001), similar to that of model 3 of this study. Some other variables were not significant, but they maintained the same sign of the regressor “age” (0.0111) and “importance of the natural resource” (0.5959).
Logarithmic model 4 was also more appropriate than model 3 for the statistical indicators of goodness of fit and Akaike criterion. In this extended model, there is a positive relationship between WTP (measured as probability) and variables such as “annual number of visits to wetlands” and “importance of wetlands”. This means that the greater the number of visits to wetlands, the greater the WTP. Also, while the greater the importance of wetlands for respondents, the greater the WTP (Table 8). Similarly, these results are similar to those reported by Zegarra (2017) in the case of Apurimac-Peru, which using the extended Bishop-Heberlein model, obtained positive signs in the relationship of the WTP with respect to age (0.012) and importance of natural resources (0.2056). In the case of income, the ratio was positive (0.7632) [19].
To calculate the measures of social welfare: average economic values, and median, the indicated formulas in Table 4 were used, taking into account estimations of model 2 suggested by Bishop-Heberlein (LOGIT Log), then selected as the model of better “adjustment” of regression. However, averages and medians of both estimated models are shown in Table 9.
Best statistical estimation of the WTP was provided by the median, which was calculated at $1.05 USD/family/month (average was $1.41 USD/family/month); this result reveals that the Ancash Region could raise approximately US $312.3 thousands per year (Table 9). Being the sample a random representative portion of Huaraz population, and considering that this population (households) is approximately 24,783 families (INEI, 2012), it could be inferred that if a homogeneous “flat” rate of $1.05 USD were applied to all families, a monthly total amount of US$ 26,022 could be collected, that being an annual value of $312,266 USD [14]. With similar assumptions, Barrantes and Flores (2013) estimated an annual collection of $739,556 USD; instead Villena and Lafuente (2013) reported that the annual WTP of the surrounding population would be between US $6.95 and US $9.45 million [10,18].
Under the assumption that the Peruvian government, private companies, and citizens should finance the costs of implementing a SEA improvement program, in equivalent amounts, and considering that approximately 67% of respondents indicated that they would pay the rate, then it would be possible to obtain up to US$ 936,797 to implement a significant SEA project in the wetlands conservation of Huaraz.
Results have indicated that most of the population consider the wetlands around Huaraz city, important ecosystems that are under threat and must be preserved to continue providing essential environment services and amenities (70% of interviewed Huaraz citizens visit the wetlands an average of 2.1 times a year). There is a large fraction of population willing to pay monetary resources for its conservation. Those who originally expressed a reluctance to pay agreed that such services should be protected or retained by “Law” and, therefore, it is up to the State to pay (35%). Another important sentiment was the distrust that the project would be successfully finished or that corruption threatens it (23%). This is a reason why authorities should enforce the possibility of the promotion of people responsibility, since this point of view was significant in the explanation of a reluctance to pay the indicated bid.
A significant inverse was the relationship between the suggested fees (bid) and the corroboration of payment; that is, the higher the rate, the lower the probability in favor of the willingness to pay, and vice versa. Other important determinants of the WTP were the perception of the importance of the interviewees regarding the conservation of wetlands, as well as the number of times the respondents visit these resources. In the latter case, the response was positive, that is to say that the greater importance the interviewees gave to the services of the wetlands, the probability of payment (WTP) naturally increases. Also, the probability of WTP increases as the number of visits to the wetland increases, suggesting the eventual need to conserve the wetlands so that they continue to provide key services to the population of Huaraz, such as provisioning, tourism, regulation of water supply, and control of erosion. This suggests that it would be necessary to sensitize the population about the ecosystem services provided by the wetlands to the Huaraz population, and with that knowledge the financing of the WTP for the creation and operation of the most viable PCBM.
From a LOGIT model adjusted to a Bishop-Heberlein functional form, the individual payment rate was estimated at US $1.05 per person (median value), with confidence limits ranging from US $0.71 to US $1.40. Assuming the possibility of a conservative payment rate, it has been considered that the median value ($1.05 USD) is the “conservative” value chosen for the prediction of the total payment amount by the citizens of Huaraz. It will be possible then a total monthly collection of $26,022 USD monthly (or $312,266 USD annual approximately), as contribution of the Huaraz population. A significant figure that could be used to constitute initial capital for the conservation and improvement of wetlands, and that could even be used to leverage national and international cooperation funds. Considering that 90% of the citizens interviewed indicated willingness to pay a minimum rate for the conservation of the environmental resource, a single payment of $1.05 USD is proposed in the electric energy bill of the population of Huaraz, pending the design of a system of management and control of the fund, with representation of groups of the social group that makes it transparent.
Economic valuation is important but it could be considered the beginning of a process that will end successfully if the steps are completed. This would be a significant figure that could be used to constitute seed capital for the conservation and improvement of wetlands, and could even be used as a basis to leverage national and international cooperation funds.
