Exact Solutions and Conservation Laws of Dissipative Hyperbolic Mean Curvature Flow for Lagrangian Graphs
The classical Lie group method is used to study dissipative hyperbolic mean curvature flow for Lagrangian graphs, then based on one-dimensional optimal system of the symmetries to the equation, the reduction equations and exact solutions are calculated. Finally, we analyze the conservation laws of dissipative hyperbolic mean curvature flow for Lagrangian graphs.
Keywords: Lie Symmetry Analysis; Exact Solutions; Dissipative Hyperbolic Mean Curvature Flow for Lagrangian Graphs; Conservation laws
Hyperbolic mean curvature flow is of great significance to geometry, modern physics, crystallography and nonlinear dynamics of surface motion. In recent years, Kong and his collaborators have made a thorough study of the hyperbolic geometric flow [1-6], for example, they demonstrated some properties of the short-time existence and nonlinear stability of hyperbolic geometric flow, and gave the lower lifetime bounds for classical solutions of hyperbolic geometric flows with asymptotically flat initial Riemannian surfaces. Kong et al introduced hyperbolic mean curvature flow in [7], and proved the unique short-time smooth solution of the flow. In [8], LeFloch et al derived the hyperbolic mean curvature flow from the principle of minimum potential energy, in the meantime, they deeply studied the conditions of the flow keeping normal motion, finally obtained a new class of hyperbolic mean curvature flow and showed some properties of this flow. In [9-10], Kong et al pointed out that the hyperbolic mean curvature flow can keep convex evolution, and found the flow will blow up in finite time or produce singularity. In [11], He et al studied the self-similar solutions of the hyperbolic mean curvature flow, and further explored that all curves contained in plane which moving in a self-similar manner under the flow are straight lines or circles. In [12], by the support function of strictly closed convex curve, Ding et al transformed the one dimensional hyperbolic inverse mean curvature into hyperbolic partial differential equation, then studied the symmetries and exact solutions of the equation by the classical Lie group method.
In [13], Duan et al investigated the hyperbolic mean curvature flow for Lagrangian graphs
Definition 1: Let (M,F) be a connected n-dimensional Finsler manifold whose fundamental function verifies F:TM → Rthe following axioms:
(F1) F(x,y)>0; ∀xεM, ∀y≠0.
(F2) F(x,λy)=|λ|F(x,y); ∀λεℝ, ∀(x,y)εTM.
(F3) the fundamental tensor gij(x,y)=(1/2)((∂²F²)/(∂yi∂yj)) is positive definite; ∀xεM,

then they differentiated both sides of this equation with respect to x, got the following nonlinear evolution equation

under the condition of the initial data were periodic, they not only proved the C3 solution to the above flow blows up in finite time, but also deduced its life-span.
In this paper, we will study dissipative hyperbolic mean curvature flow for Lagrangian graphs

then we can obtain the following nonlinear evolution equation
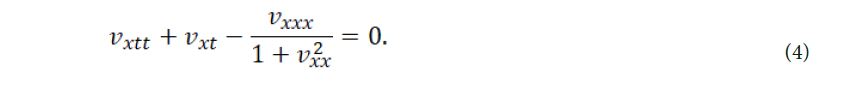
The aim of this paper is to find symmetries of dissipative hyperbolic mean curvature flow for Lagrangian graphs via the classical Lie group method [14-17]. Then we investigate one-dimensional optimal system of the symmetries to the flow by using the method in [18]. After solving the reduction equations, we calculate the exact solutions of the flow. Based on the method and thought provided by Ibragimov [19], we obtain conservation laws of dissipative hyperbolic mean curvature flow for Lagrangian graphs.
In the end, this paper is arranged as follows. Section 2, we mainly discuss Lie symmetries of dissipative hyperbolic mean curvature flow for Lagrangian graphs. Section 3, the exact solutions of the flow are obtained by solving the reduction equations. Section 4, conservation laws have been set up. In the last part, conclusions are made in Section 5.
In this part, we suppose

so eq. (4) becomes

we use classical Lie symmetry analysis for eq. (6) and consider a transformation group with one parameter
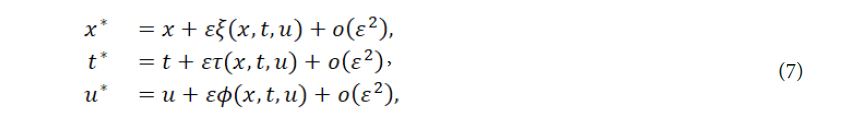
in which ξ(x, t, u ), τ(x, t, u ), φ(x, t, u ) are all arbitrary functions of x, t, u and is an infinitesimal parameter. The infinitesimal vector field of eq. (6) is
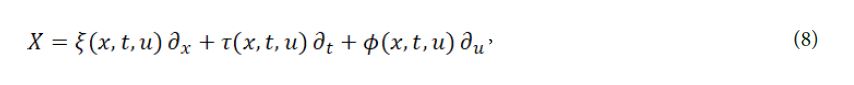
the form of the second order extension of infinitesimal algebra is
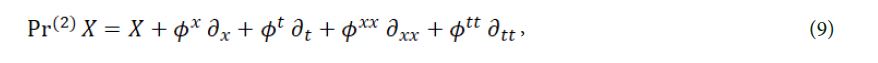
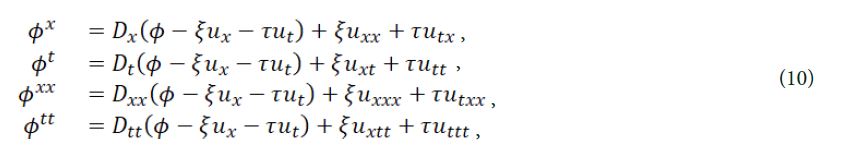
from the condition of invariance, we have
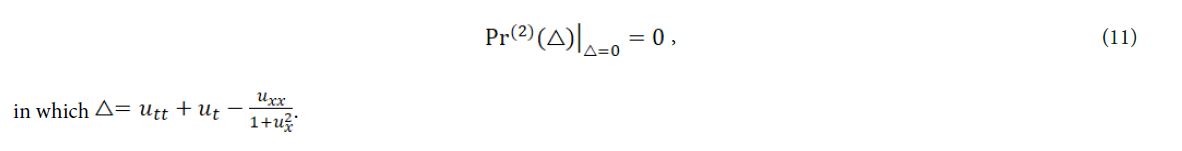
By solving eq. (11), we can get the overdetermined equations of eq. (6),
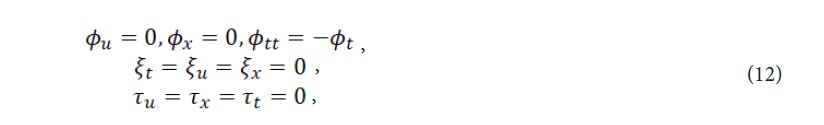
then solving the above equations, we have

where c1, c2, c3, c4 are arbitrary constants. The corresponding infinitesimal generator of eq. (2) is
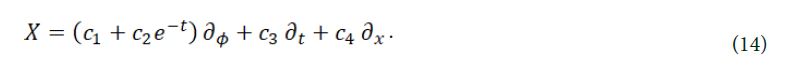
So the infinitesimal generators of eq. (6) are spanned by

The Lie transformation groups corresponding to the following generators are calculated and their initial value problems are considered
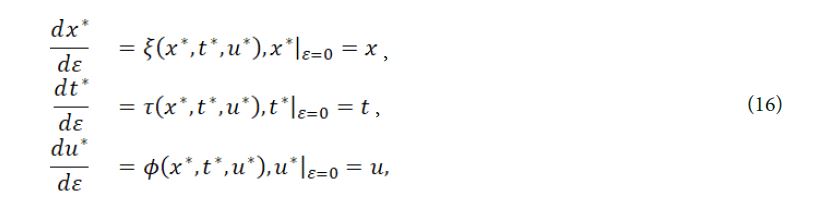
the corresponding single parameter group are obtained by solving the above vector fields,
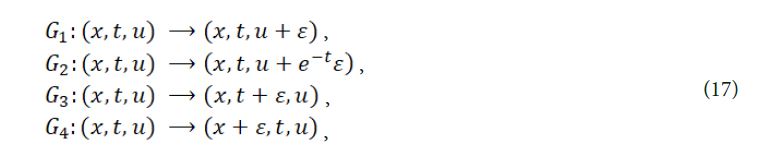
so from the single parameter group Gi(i= 1,2,3,4) in (17), the expression of the solution of the eq. (6) can be obtained:

According to the definition of Lie bracket and adjoint representation,

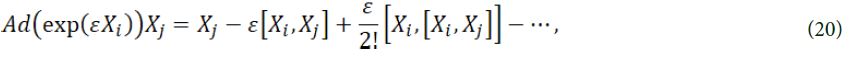
we can get Table 1 and Table 2 respectively.
Next, we are going to use Table 2 to give the classification of subalgebras for eq. (6), assume a vector
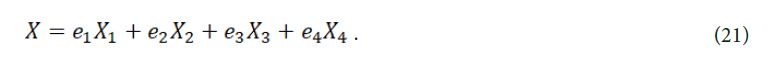
Firstly, we suppose e3 ≠ 0, we select e3 = 1, (21) becomes

we apply to Ad(exp(e2)x2), so the coefficients of x2 can be eliminated,
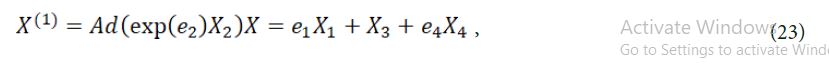
that is to say, when e3 ≠ 0, X is equivalent to X(1) = X3 + e1X1 + e4X4.
The rest of one-dimensional subalgebras are generated by X with e3 = 0, X is equivalent to X(2) = e1X1 + e2X2 + e4X4.
Based on the above discussion, we obtain the following theorem.
Theorem 3.1. Ane-dimensional subalgebras of the 4-dimensional Lie algebra is spanned by:
Can be made without changing anything essential. Where Ψ is a wave function and λ is an arbitrary function of space and time. (10) Is called a local gauge transformation
X3, X3 ± X1, X3 ± X4, X3 ± X1 ± X4, e3 ≠ 0
X1, X2, X4, X1 ± X2, X1 ± X4, X2 ± X4, X1 ± X2 ± X4, e3 ≠ 0
In this part, we mainly seek the similar reduction and invariant solutions of eq. (4).
Case 1: X2 = ∂t. By solving the characteristic equation

we get the group-invariant solution

where s = x. Taking (25) into eq. (6), we have

by solving eq. (26), we can get
.
So

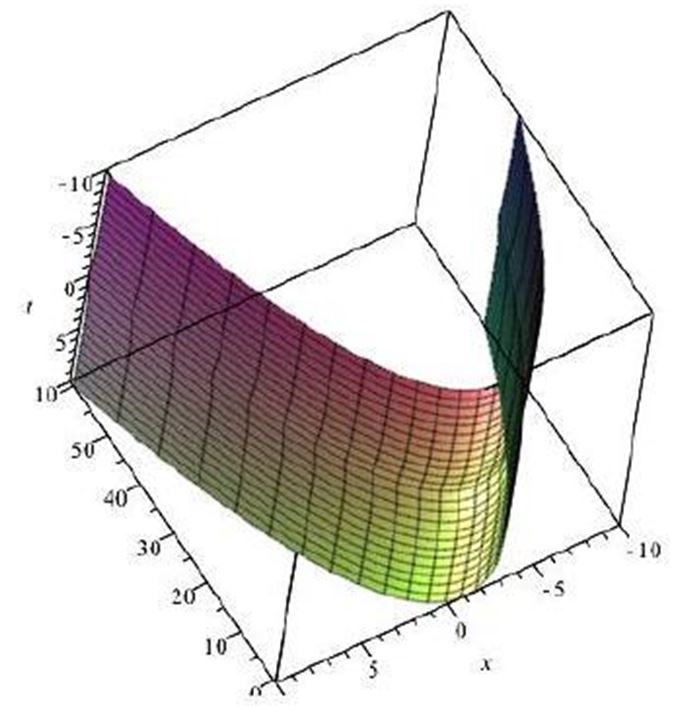
therefore eq. (4) has a solution
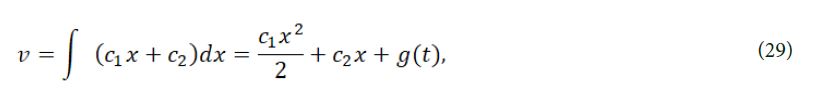
where g(t) is an arbitrary functions about . The graph of (29) for
C1 = 1, C2 = 1, g(t) = sech(t),
is shown in Figure 1.
Case 2: X2 + X4 = e-t∂u + ∂x. Solving the characteristic equation

the group-invariant solution is

where s = t. Taking (31) into eq. (6), we get

solving eq. (32),


so we can get
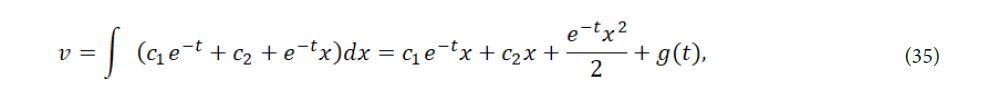
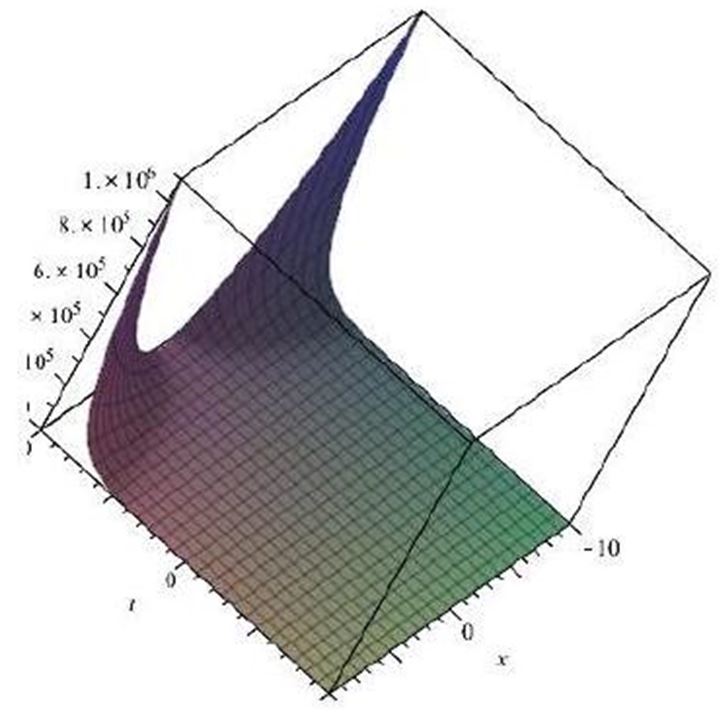
where g(t) is an arbitrary functions about . The graph of (35) for
C1 = 0, C2 = 1, g(t) = sin(t),
is shown in Figure 2.
Case 3: X1 + X3 + X4 = ∂u + ∂t + ∂x. The characteristic equation is

by solving eq. (36), we have

where s = t - x. Taking (37) into eq. (6), eq. (6) reduces into

then we suppose fs = y, eq. (38) becomes

then we can find that the general solution of eq. (39) is
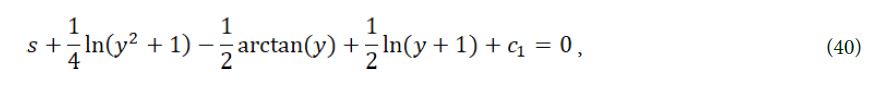
if is solved, we can get

So
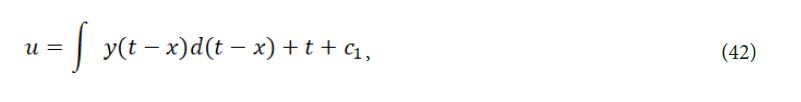
finally, we obtain solution of eq. (4) as shown
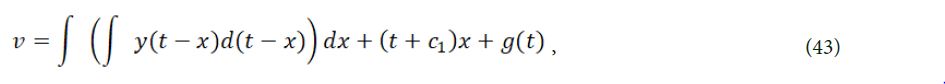
where g(t) is an arbitrary functions about .
Case 4: X3 + X4 = ∂x + ∂t. The characteristic equation is

where s = t - x. Taking (44) into eq. (6), eq. (6) reduces into

then we suppose fs = y, eq. (45) becomes

solving it, we can get

so we can get
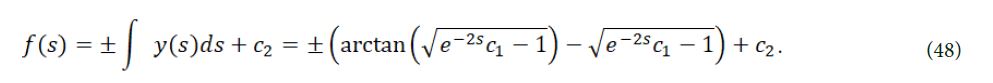
So
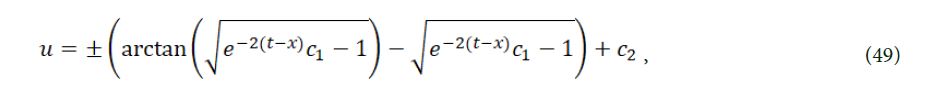
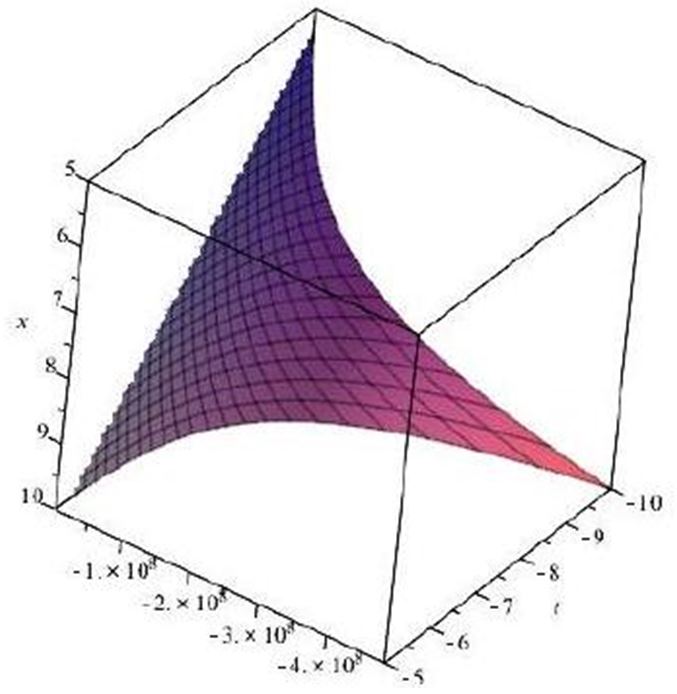
therefore, we acquire the solution of eq. (4)

where g(t) is an arbitrary functions about . The graph of (50) for
C1 = 1, C2 = 0, g(t) = sin(t),
is shown in Figure 3.
Case 5: X1 + X3 = ∂t + ∂u. Solving the characteristic equation, we have

where s = x. Taking (51) into eq. (6), eq. (6) becomes

solving (52), we get
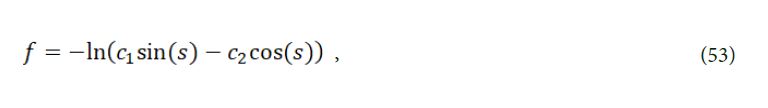
so
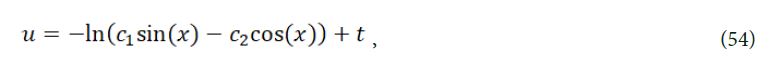
therefore eq. (4) has a solution as

where g(t) is an arbitrary functions about .
In this section, we are going to calculate the conservation laws of eq. (4). Suppose the standard Lagrange function of eq. (4) is
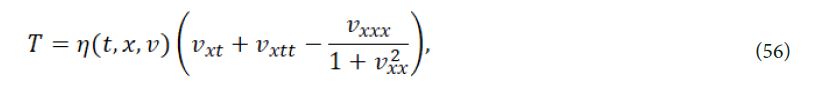
where η(t,x,v) is the conservation law multiplier, it can be given by the following determining equation

δ/δv is the Euler-Lagrange operator, and its expression is
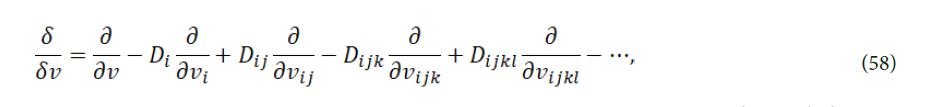
by solving eq. (57), we get

solving the above equations, we get

where h(t) is an arbitrary functions about . Here we select

So

The conserved vector is given by C = (Cx,Ct), where
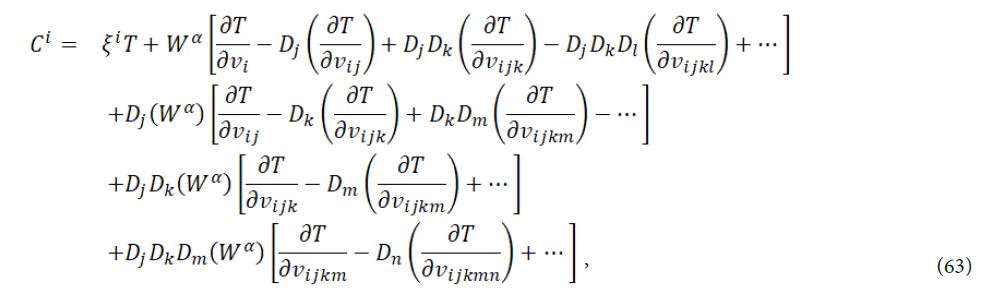
where Wα = ηα - ξi υαj. The conservation law for eq. (4) is determined by the following formula:

where
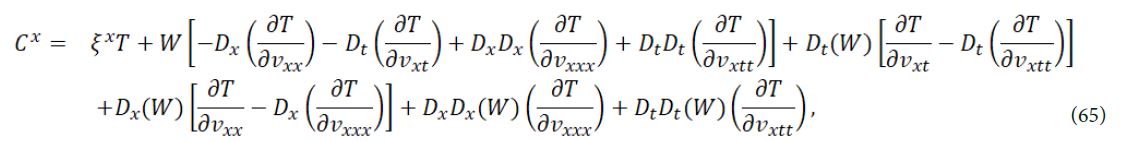

Let’s take the vector field X3 as an example:


In this paper, the Lie symmetry analysis is performed on dissipative hyperbolic mean curvature flow for Lagrangian graphs, then by solving the reduction equations, the exact solutions of the flow are carried out. Eventually, the conservation laws of dissipative hyperbolic mean curvature flow for Lagrangian graphs are solved.
Remark 1: Compared with [11], He et al concerned the self-similar solutions to the hyperbolic mean curvature flow for plane curves. They proved that all curves immersed in the plane which move in a self-similar manner under the hyperbolic mean curvature flow are straight lines and circles. Compared with [12] and [17], we studied different equations by using Lie group method, and the ways to find the optimal system were different. Compared with [13], Duan et al assumed the initial data were periodic, then they found the C3 solution to the hyperbolic mean curvature flow for Lagrangian graphs must blow up in finite time and the lifespan can be also derived.
The author is very grateful for the teacher’s patient help and the referees’ valuable advice. This work was supported by Young Scientists Fund (CN) (Grant No. 1100115, No. 11201473), Natural Science Foundation of Shandong Province (Grant ZR2021MA084), and the Natural Science Foundation of Liaocheng University (318012025).