Optimization of The Binary Interaction Coefficient Kij for Calculating the Solubility of Drug Compounds in Co2 Using a Genetic Algorithm

Any separation operation is one of the most important elements in the field of process engineering. However, their performance depends greatly on the operating conditions of pressure, temperature, etc. The knowledge of these conditions experimentally is not always easy to achieve. It is therefore essential to have computational models capable of predicting as efficiently as possible the equilibrium between phases up to the critical point.

High pressure solid-liquid phase equilibrium calculations are important for the modeling and design of processes that use supercritical fluids to selectively extract dissolved solids. These supercritical fluids have a wide range of applications, particularly in separation processes. The determination of the solubility of the solute in the supercritical fluid is the key parameter in the calculation or design of such processes. The calculation is often performed using a cubic equation of state (EOS).

When an equation of state is applied to mixtures, molecular interactions are taken into account through a binary interaction coefficient, called k_ij, whose determination is very delicate, even for simple mixtures.

Therefore, the present study is mainly concerned with two main points:

1) The problem of choosing the most appropriate Equation of State (EOS)-Mixing Rule (MR) combination to estimate the solubility of four new solid pharmaceutical compounds, benzamide, cetirizine, metaxalone and niflumic acid in supercritical CO₂ at different temperatures and pressures ranging from 100 to 400 bar.
2) The determination of the binary interaction parameter k_ij using a concept of group contribution as a function of temperature directly.

The opportunity was taken to insert new groups in the interaction parameters matrix using an optimization technique based on the genetic algorithm and also to extend the predictive concept to other equations of state such as Peng-Robinson, Redlich Kwong Soave.

The thermodynamic models were tested on different systems mainly hydrocarbons and CO₂, knowing that the new groups introduced are: CO, NH₂, NHcyc, O, Ocyc, Co, F, NH, Ncyc , Clcyc , OH.

Keywords: Supercritical Fluid; Equation of State; Phase Equilibrium; High Pressure; Genetic Algorithm; Binary Interaction Coefficient

a. Supercritical CO₂

Supercritical fluids (SCF) are the subject of several research works, both at the fundamental and applied levels. The major interest of these fluids lies in the possibility of modulating and adjusting their physico-chemical properties from the gaseous state to the liquid state (density, transport properties...). The processes using them are diverse and of growing interest in many sectors. Carbon dioxide (CO₂) is the most widely used supercritical fluid. This is due to the fact that CO₂ is cheap, chemically inert, non-toxic, non-flammable and readily available in high purity and low cost. Moreover, the critical point of CO₂ is easily accessible (critical temperature of 304.2 K and critical pressure of 73.8 bar).

b. Solid Compounds Drugs

Various solid compounds are used to make drugs in the pharmaceutical industry. Many of these compounds are extracted from herbs using different technologies, including supercritical fluid extraction. The determination of the solubility of these solid compounds is of great importance in the pharmaceutical industry. Despite all the advantages of SCF technology, the experimental procedure of solid solubility determination in a supercritical fluid can be time consuming and expensive. Therefore, studies have been conducted to model and correlate the solubility of a solid solute in a supercritical fluid. To date, research on the solubility and modeling of drug compounds is scarce.

Benzamide is used to make trimethobenzamide which treats nausea and vomiting related to surgery or caused by stomach flu. It is also used to study the photo-catalytic decomposition mechanisms of aqueous solutions of acetic acid, acetamide and acetonitrile in the presence of semiconductors.

Cetirizine is an antihistamine used to relieve allergy symptoms, i.e. allergic rhinitis, hay fever, and hives, such as watery eyes, runny nose, itchy eyes/nose, sneezing and itching.

Metaxalone is a muscle relaxant used to relax muscles and relieve pain caused by strains, sprains and other musculoskeletal conditions. It is considered a moderately strong muscle relaxant, with a relatively low incidence of effects.

Niflumic acid is a drug used for joint and muscle pain. In addition to anti-inflammatory actions, they have analgesic, antipyretic and antiplatelet properties.

Applying the is fugacity criteria in both phases and disregarding any influence of pressure on the volume, the solubility of a pure organic solute in supercritical carbon dioxide is expressed as below:

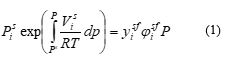
with P and P^s_i the prevailing pressure and sublimation vapor pressure of the solute at a given temperature T, respectively, ϕ^fs_i the fugacity coefficient of pure solute in the supercritical phase, P^s_i the solute molar volume at its vapor pressure, y^fs_i the solute solubility in the supercritical carbon dioxide, T the prevailing temperature and R the universal gas constant.

Usual common two parameters equations of state can be expressed by the following general equation [2,3]:

The two well-known equations of state i.e. those of Peng-Robinson and Soave are obtained with u and w taking integer values as shown in Table 2. The parameters a and b are calculated in terms of critical properties as also shown in Table 2.

Two mixing rules were tested in the present work and are described as follows:

• The van der Waals MR: the mixing parameters are expressed as follows [3,4,5,6,7]:

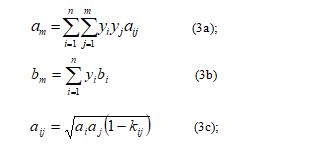
The Panagiotopoulos-Reid (P-R) MR : despite the fact that it is complicated compared to the standard ones such as that of van der Waals, it has been considered in many applications. Its parameters are expressed as follows [1]:

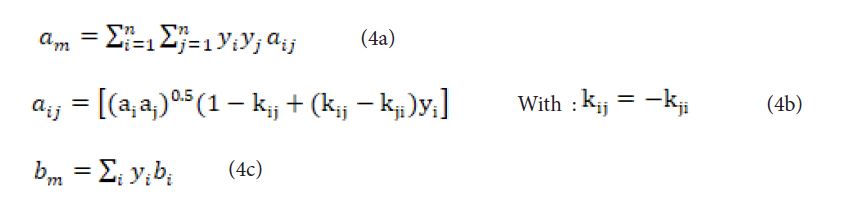
k_ij is an interaction parameter. The fugacity coefficient can be expressed in a general manner as [2]:

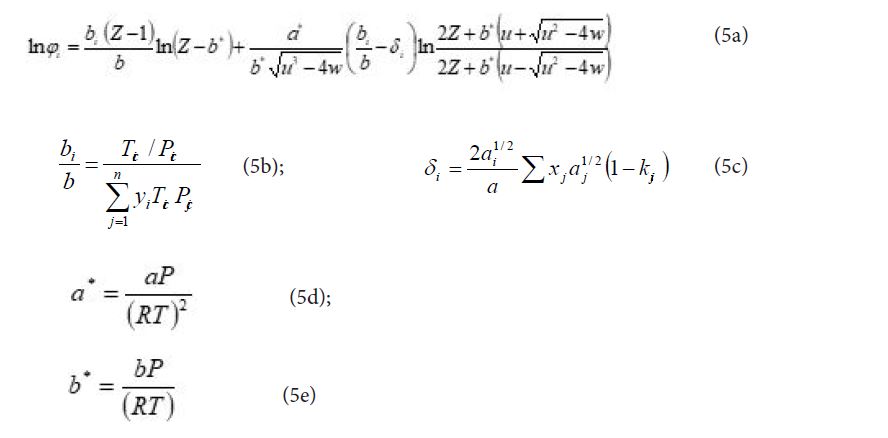
The molecular interactions are taken into account by a binary interaction parameter, called k_ij which it is proposed in this work to estimate by a group contribution method, exploiting the fact that it depends only on the temperature of the mixture and that its calculation does not require the knowledge of other properties than those required by the equation of state, i.e. the critical properties such as the critical temperature, the critical pressure as well as the acentric factor of the pure bodies constituting the mixture.

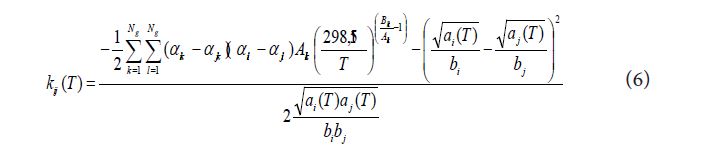
With T the temperature, a_i and b_i parameters to be calculated according to the considered equation of state, N_g the number of the different groups involved, α_ik the fraction of molecule i occupied by group k (number of groups k in molecule i divided by the total number of groups in molecule i), A_kl and B_kl constant parameters with A_kl = A_lk and B_kl = B_lk (k and l being two different groups and A_kk = B_kk = 0).

So in addition to the critical properties and acentric factors that are needed to calculate the a_i and b_i parameters, it is also necessary to know the decomposition of each molecule into elementary groups to have the α_ik and thus the k_ij.

The choice of the equation of state and the mixing rules used was made and the expression of the binary interaction coefficient as a function of the group decomposition of the molecules was established, it now remains to examine the problem of defining the elementary groups of the model.

Indeed, when implementing the group contribution method considered, the main difficulty lies in the realization of the division of the molecules into elementary groups because there is no general rule until now. However, two quite important things are increasingly used in the decomposition of a molecule into elementary groups: it is the nature of the group itself, its position in the molecule (neighboring groups, proximity effects, etc.) and the character of this same parent molecule (linear, branched, aromatic, etc.).

In the literature, the first six elementary groups introduced in the models intended for the calculation of the interaction parameter k_ij are from alkanes (linear and branched) and are:

1 = CH₃, 2 = CH₂, 3 = CH, 4 = C, 5 = CH₄ (methane), 6 = C₂H₆ (ethane). It is clear that the first two terms of the alkane series each constitute an elementary group [19- 22].

In order to introduce other groups, aromatic hydrocarbons were considered and allowed the introduction of three new groups which are: 7 = CH_aro, 8 = C_aro et 9 = C_polyaro. The latter is found in poly-aromatic molecules such as naphthalene or phenanthrene [19- 22].

Then saturated cyclic hydrocarbons were considered, allowing to involve two other groups which are: 10 = CH2, cyclic and 11 = CH_cyclic or C_cyclic [19- 22].

Finally applications involving supercritical carbon dioxide, such as the extraction of essential oils, encouraged the introduction of CO₂ as the twelfth group [19- 22].

Table 3 therefore summarizes the list of all elementary groups used in the literature, which are as follows:

The binary interaction coefficient k_ij involved in the mixing rules is calculated by a method of group contributions whose literal expression is given by equation (6) and whose use depends on the availability of two parameters (A_kl and B_kl).

However, the determination of these two parameters is not easy and requires fairly robust optimization methods capable of leading to fairly accurate solutions. Therefore, in this article, an optimization method based on the genetic algorithm is used because of its ability to converge to the optimum even in the case of quite complex problems and because of its simplicity and ease to be inserted in a computational code in FORTRAN language.

Genetic algorithms provide solutions to problems that do not have solutions that can be computed analytically or algorithmically in a reasonable time. In this method, thousands of more or less good solutions (genotypes) are randomly created and then subjected to a process of evaluation of the suitability of the solution mimicking the evolution of species where the most adequate and optimal ones with respect to the problem survive more than the less adequate ones, Hence the evolution of the population by successive generations by crossing the best solutions and mutating them, repeating this process a certain number of times with the aim of reaching the optimal solution [48- 50].

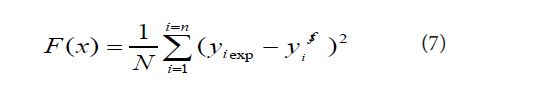
Genetic algorithms adopt the principle of Darwinian evolution of biological populations where a population of well-defined size where each individual is coded into a string of characters (chromosomes), is randomly initialized at the beginning of the algorithm. The population evolves over generations by applying to each generation a process analogous to natural selection. The most adapted individuals go to reproduction while the least adapted ones disappear before. The genetic operators of crossing and mutation are then applied to the selected population.

During the crossing over process, two chromosomes exchange parts of their chains to give new chromosomes. This crossing can be single or multiple. The maximum rate of individuals that can interbreed is controlled by an interbreeding probability. As a rule, the proportion of occurrence is set to 0.8 in a classical genetic algorithm [48].

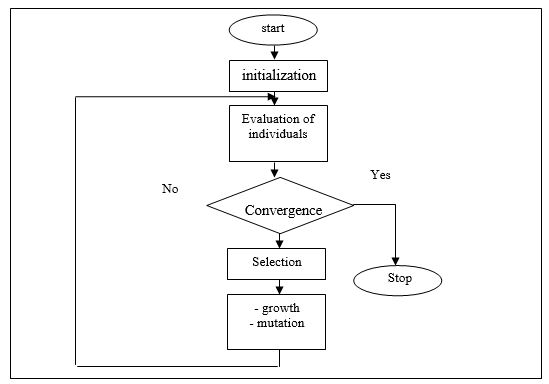
In a random way, a gene can, within a chromosome, be substituted for another one. This is what is known as the mutation process. In the same way as for crossover, a parameter (probability) that controls the mutation rate is also defined. Genetic operators, whose task is to explore the design domain in order to find the global optimum, generate a new population that performs better than the population of the previous generation? This exploration ends by verifying a convergence test whose nature will be specified later. The classical architecture synthesizing the main steps implemented in a genetic algorithm is presented on the flowchart of figure 1, above

Based on the theoretical developments presented in the previous paragraphs, and for the estimation of A_kl, B_kl, a calculation code has been developed with the FORTRAN programming language.

Finally, the steps of the genetic algorithm are summarized as follows:

1. Generate a population of individuals of size N: x1, x2, x3,..., xN.
2. Calculate the chances of survival (quality or fitness) of each individual: f(x1), f(x2), f (x3) ..., f(xN).
3. Check if the termination criterion is met. If yes, go to stop.
4. Choose a pair of individuals for reproduction (according to the chances of survival of each individual).
5. According to the probabilities associated with each genetic operator, apply these operators.
6. Place the individuals produced in the new population.
7. Check if the new population size is correct. If not, return to step 4.
8. Replace the old population of individuals with the new one.
9. Return to step 2.

This work can consist of a determination of the solubility of solid compounds in SC - CO₂, then an optimization with a genetic algorithm that allows to determine precisely the binary interaction parameter for the modeling. The thermodynamic behavior of these highly asymmetric systems is described by different proposed models which, generally, involved a combination of an equation of state (EOS) with a mixing rule (MR).

Four new solid pharmaceutical compounds considered in this study are benzamide, ketrizine, metaxalone and niflumic acid. All four compounds are classified as drugs.

All the results obtained concerning the modeling and that of the interaction parameter, are presented and discussed by comparison, according to availability, with experimental values reported in the literature.

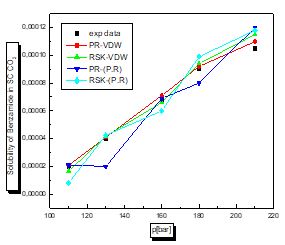
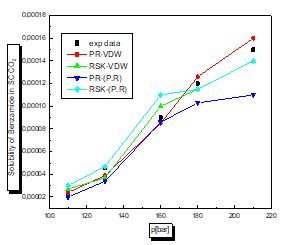
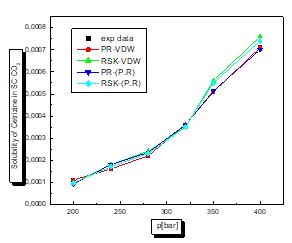
For this case according to the figures and table above, the results are reasonable well for the model PR78 (EOS)-VW (MR). It can be seen for organic solutes in supercritical CO2 that a small value of kij leads to the best results. The PR78-VDW model seems to be the most reliable compared to the others. This is also true for other organic solutions.

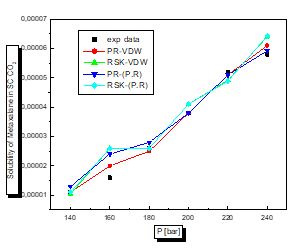
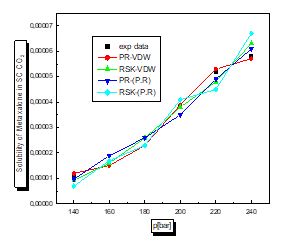
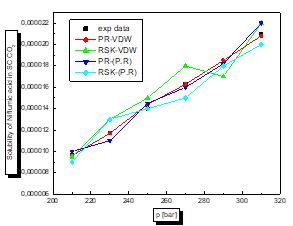
There is a proportional relationship between solubility and pressure for the four pharmaceutical compounds.

The interaction parameters between groups obtained by executing a program in FORTRAN language are grouped together in the form of different matrix.

The parameters of interaction between molecules are used for the calculation of the solubility of the benzamid, cetirizine, Metaxalone and niflumic acid in supercritical CO2 , the different results obtained by the different equation combinations of the mixing rule of states are all compared to the experimental values on Fig 2 to figure 9.

New extraction technologies that are cost effective and comply with both environmental pressures and consumer preference are becoming more popular. Supercritical carbon dioxide extraction is one of the most efficient methodologies that has found a great variety of applications in recent years.

Various solid compounds are used for making drugs in pharmaceutical industry. Many of these compounds are extracted from herbs using different technologies, including the supercritical fluid extraction. Determining the solubility of these solid compounds is of great importance in the drug industry. Despite all of the benefits of SCF technology, the experimental procedure of determining solid solubility in supercritical fluid can be time consuming and expensive. Consequently, studies have been made to model and correlate the solubility of solid solute in supercritical fluid.

In this study, an effect of equations of state and mixing rules in a thermodynamic approach has been investigated for correlation of solubility of four new solid pharmaceutical compounds, namely, benzamide, cetirizine, metaxalone and niflumic acid in supercritical CO2 at different temperatures and pressures. Two equations of state of Peng-Robinson (PR) and Soave-RedlichKwong (SRK) coupled with mixing rules of one-parameter van der Waals and P.R, where the binary interaction parameters for these sets of equations were evaluated by equation 6 and by different matrix (Table 4 to 7).

The fourth thermodynamic models are assessed according to the AARD as shown in Table 8.1 -8.8 where PR-VDW and PR- (P.R) provide the best combinations

which:

where N is the number of measurement points, yi exp and yi calc are the experimental and calculated amounts of solubility, respectively.

The results of thermodynamic modeling using different EOS and mixing rules are in good agreement with experimental data for the investigated conditions of components. Solubility data for all compounds show an increase with rising pressure at constant temperature. With increasing pressure, the intermolecular distance reduces, and hence the density of supercritical CO2 increases.

The solubility increases with temperature at constant pressure. Increasing the temperature has two inverse effects. First, it increases density, and hence decreases the solvating strength. However, the solid vapor pressure increases with temperature.

In most figures, the differences between experimental data and four various correlated results are less at lower pressures and become greater at higher pressures. This is due to the weakness of cubic equations of state for calculation of solid solubility in SCF at high pressure.

Experimental solubility data for benzamide, cetirizine, Metaxalone and Niflumic acid in supercritical CO2 were taken from [16-19] respectively.

Through this study, the importance and complexity of modeling processes involving high pressure processes have been highlighted. It is based on different equations of state to which are associated different mixing rules. The equations of state involve a binary interaction parameter kij which is not always available and whose influence on the accuracy of the phase equilibrium data has been demonstrated in this work.

Still in this perspective of further developing this approach, new systems have been considered in order to involve new elementary groups and enlarge the matrix of interaction parameters, for the calculation of solid-liquid equilibrium at high pressure. An optimization method based on the genetic algorithm was used to calculate the new interaction parameters, highlighting the capabilities of this algorithm.

The comparison between the results of the present work and those reported in the literature is encouraging, as well as the new models based on the method of contribution of the groups have led to quite accurate results.

Mixing Rule combination for a given system; the determination of the binary interaction parameters by means of a group contribution concept in terms of temperature directly and the extension of the 12-group matrix using GA.

The thermodynamic modeling results using the different EOS and mixing rules are in good accordance with the experimental data for the studied component conditions.

The model provides a better correlation than conventional models that use the Predictive PR-State Equation with the VDW MR mixing rule.