Relationship between Structures of C5C7 Carbon Nanotubes and Geometry of Ornamental
Many medieval Islamic mosques and palaces are adorned with highly intricate geometric ornaments. These decorations have inspired modern artists and art historians, and they have been discussed in connection with modern mathematical concepts such as crystallographic groups and aperiodic tiling. The Islamic ornamental patterns can certainly be used to illustrate such modern notions.
Carbon nanotubes are molecular-scale tubes of graphitic carbon with outstanding properties. They are among the stiffest and strongest fibers known and have remarkable electronic properties and many other unique characteristics. For these reasons, they have attracted huge academic and industrial interest, with thousands of papers on nanotubes being published every year, though commercial applications have been rather slowly developing, primarily because of the high production costs of better quality nanotubes. A topological index of a graph G is a numeric quantity related to G. The oldest topological index is the Wiener index. Its numerous chemical applications were reported and its mathematical properties are well understood.
The numbers 5 and 7 and the shapes of a pentagon and a heptagon have important historical and symbolic connections. These two shapes have been frequently used in art and architecture especially in ornamental patterns of Islamic art and architecture. The form of the HC5C7 nanotube is a composition produced from the neighborhood of the pentagon and the heptagon.
Keywords: Carbon nanotube; HC5C7 nanotube; Geometry of ornamental; Symmetry
In this article, we are going to look at structures of carbon Nanotubes of the type C5C7. In fact, we examine the role of these structures in the nature and everyday life of humans. These structures are very functional so, they play a huge role in the pursuit of human beings. Usually, in non-laboratory conditions, they appear as diamonds in nature. Individually, they also form part of the basic components i.e. the pentagonal and hexagonal structure is individually available in diamonds. Of course, they can also form a diamond structure horizontally, vertically and wholly when they are together. Because of all natural structures play a vital role in human life, so affect lifestyle. Many of the old symbols and signs of human life are inspired by these natural carbon structures. The traditional architecture of the old countries of the world has also been used. Because these structures are actually graphs of mathematics, then proof of the correctness and the existing relationship can always be pointed out. In articles it is mentioned [1-6]. In this article we will explain the relationship between structures of C5C7 Carbon Nanotubes and geometry of ornamental.
In articles mentioned in the reference from this author, we tried to find the relationship between structures of C5C7 Carbon Nanotubes and mathematics and formulate its indexes [3-7]. In this paper, the method is as follows, first, by introducing natural and existing structures in nature, we identify them and then check the use of these forms in traditional and modern architecture, symbols and other unrelated signs.
From the traditional viewpoint, five symbolizes a human being represented by a pentagon. Five is the number of divine marriage (hieros gamos), being a result of female (the even number 2) and male (the odd number 3). Five is the number of center and intersection of the heaven and the earth and also shows four directions plus center as well. Number five symbolizes meditation, religion, mediation, and variability [8-10]. Pentapetalous flowers and pentad leaves such as rose, lily, and pine are symbols of microcosm. In Islamic tradition, five symbolizes the five pillars of religion (prayer, fasting, tithe, zakat, and jihad), the principles of Shiism (monotheism, prophet hood, resurrection, justice, and the imamate), five-fold prayers (morning, midday, afternoon, sunset, and esha’), five pure persons of the Household (according to hadith of Kasa’: Muhammad, Ali, Fatima, Hassan, and Hossein (AS)); “Khoms” (religious obligation of giving one-fifth of wealth to the poor and needy families); also in Islamic mysticism, it is the symbol of five divine Presences or the manifestation hierarchy of the Truth (Hahut: absolute unseen, pure absolute, being, existential principle; Jabarut: world of angels, supra formal manifestation; Malakut: world of dominion, purgatory world, tender formal manifestation; Nasut: the world of matter, sensible world, dirty formal manifestation) [8].
In Christian tradition, five is the symbol of humanity after his fall, five senses, five points of the Cross, and five injured of Christ. In Hebrew tradition, five means strength. In China, there are five elements, five barley, five stages, five planets, five sacred mountains, five colors, five flavors, and five main virtues, the number of divine blessings and eternal ideas and human relations is also five. In Hindu tradition, also, there are five worlds, five tender elements, and five rough elements; primary colors and tastes are also five. Among Pythagoreans, Five embodies the divine union, the marriage of heaven and earth, and the light.
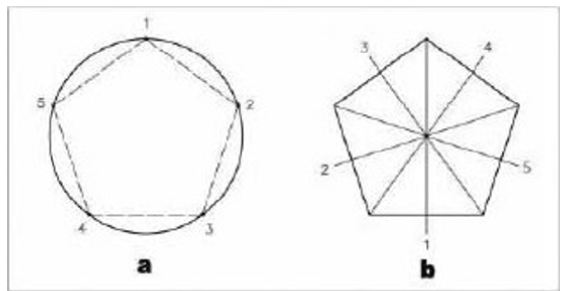
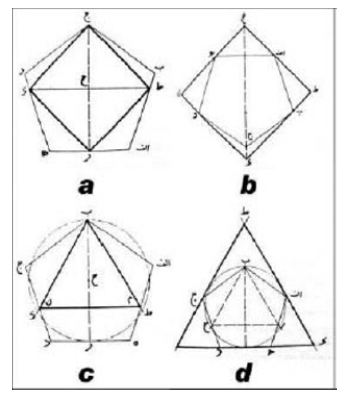
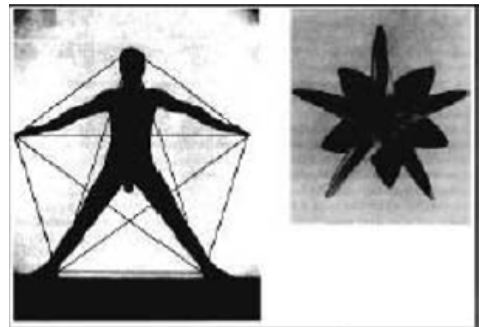
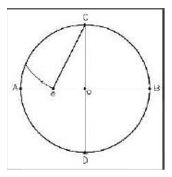
If a circle’s perimeter is divided into five equal divisions and the points of divisions, respectively, are connected with each other, the result is a pentagon (Figure 1). This shape is one of the regular polygons, so all its interior angles and all sides are equal. The pentagon has five apexes, five sides, and five symmetry axes that cross over each apex and the middle of its opposite side, and are perpendicular with the side; they also meet each other at the center, L⊥AB and ab ‖ ec).
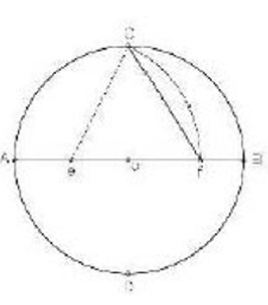
The measure of interior angles of the pentagon is 108° For drawing an inscribed pentagon of a circle and dividing the circle perimeter into five equal parts, first, draw two perpendicular diameters of the circle (AB and CD). Then determine the middle point of radius OA (point E). Then draw an arc with center E and radius CE to cut the radius OB of the primary circle at point F. CF is equal to the side of the inscribed pentagon of the circle, or 1/5 of the circle’s perimeter (Figure 2 and 3).
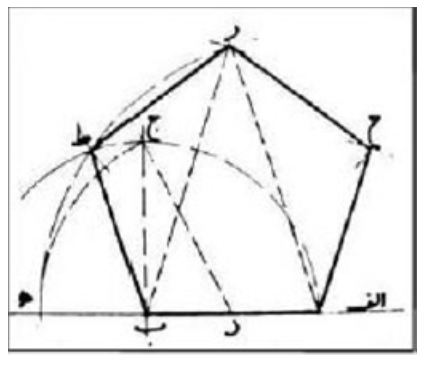
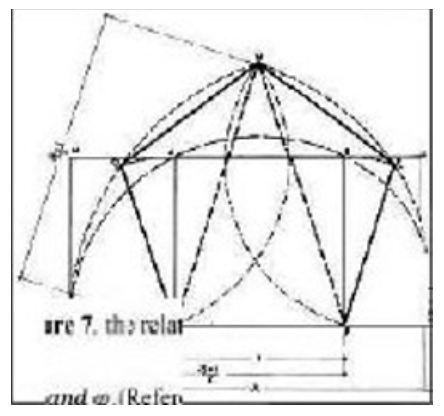
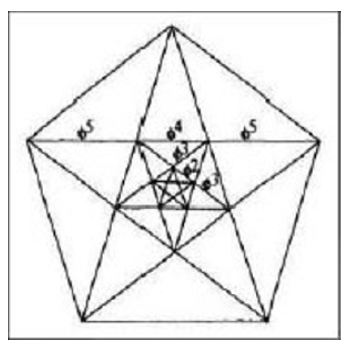
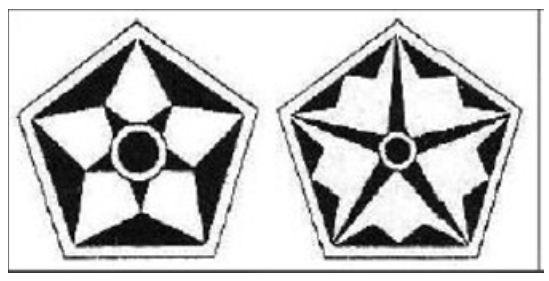
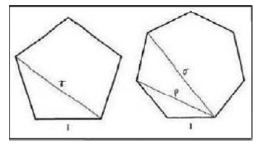
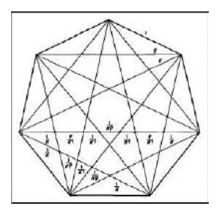
If any points of divisions is connected to its first lateral point, the result is the pentagon, and if it is connected with the second lateral points, the result will be the pentagram. If all these points are connected to each other, i.e., each point is connected to the remaining four points, a combination of pentagon and pentagram will be achieved (Figure 4a-c). A pentagram has a direct relationship with a pentagon. If the sides of a pentagon are extended to cut each other, a pentagram will be produced (Figure 2a). If the middle of the sides of a pentagon are respectively connected to each other, a smaller pentagon will emerge. If the construction is continued, we will have a harmonic series of diminishing pentagons in a geometric form (Figure 2c). This, in the case of a pentagram, it is also valid (Figure 5 and 6). The method of drawing a pentagon is shown in Figure 5, and the method of Albuzjani for circumscribing a pentagon on and inscribing a pentagon in a triangle and square is shown in Figure 7.
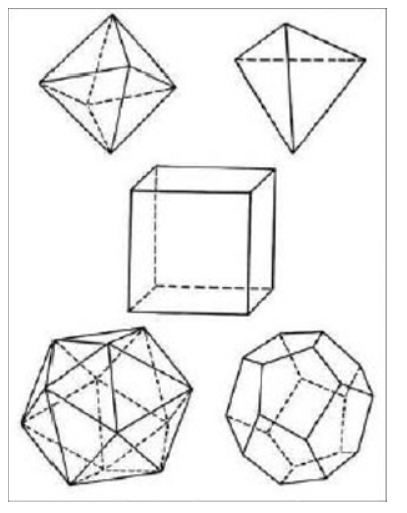
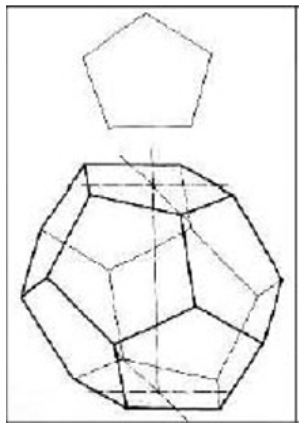
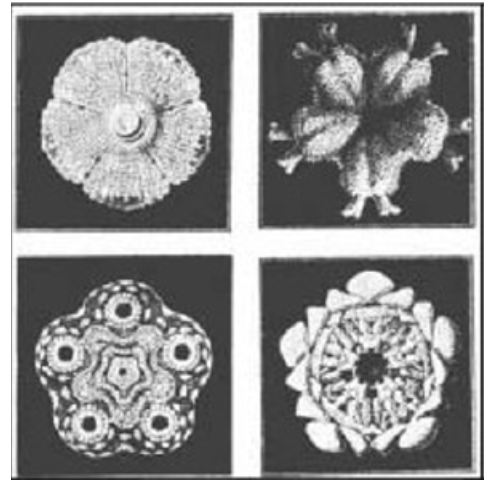
A relationship between a pentagon and √5 is shown in 6 and a relationship between a pentagon and ϕ is shown in Figure 8. The dodecahedron, the fifth volume of Plato solids after the tetrahedron, octahedron, cube, and icosahedron, consists of twelve pentagons (Figure 9 and 10). “The pentagonal dodecahedron, traditionally related to the universe by Plato in his cosmological treatise Timaeus, is included in the Islamic philosophical perspective by Al-kindi” (see [16]). Also, the volume of Albuzjani, a Muslim mathematician of the 14th century, composed of pentagons and hexagons is shown in Figure 10. The applications of five and pentagon in the geometry of life, nature, and humans, is shown in Figure 11, Figure 12 Figure 13 Figure 14. Also, pentagonal proportion has been observed in some artworks like the statue of the head of Hermes and in architectural section of the Osiris temple (Figure 15 and 16).
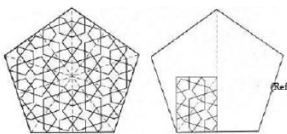
Pentagons and pentagrams and shapes resulting from them, i.e., decagons and 10-fold stars, have rich applications in ornamental patterns and designs of architecture of different civilizations, and they were frequently used in Islamic architecture in particular. In this section, only some samples are given. Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 show applications of the mentioned shapes in knot works, tile works, mosaics, and tessellations (floor coverings) (Figure 17 and 18).
From the traditional viewpoint, seven is the number of the world, completeness, and integrity, and with three heavens and souls and four earths and bodies, it is the first number that is both material and spiritual. Seven symbolizes perfection, security, safety, peace, abundance, reunification, synthesis, and virginity. Seven is also the symbol of seven floors of the universe, heavens, hells, big planets, and metals associated with them, circles of the universe, lights of the sun, the intelligence pillars, lunar parts of the rainbow, days of the week, the music notes, seven-fold wonders, etc. According to Philo, the seventh power of any number is both square and cube, and hence has high importance.
In Islamic tradition, seven is the first complete number, and also, there are seven heavens, seven lands, earths, seas, and colors. The number of active forces and heart stages is seven. Seven times circling around Ka’ba’, symbolize the seven signs of the god. In Christian tradition, the god is shown with the seventh light in the middle of six lights of the creation. Seven is also the symbol of seven sacred religions, gifts of spirits, deadly sins, classes or mountains of purgatory, prophets who are possessors of firm resolve, angels of exalted presence, devils that Christ (AS) drove out, the period of fasting and repentance, joys and sufferings of Mary (AS), and heroes of Christianity. In Hebrew, seven is the symbol of eternal wisdom, also there are, in the Jewish year, seven great and sacred days, and the Heykal was built in seven years.
In Hinduism, Seven symbolizes the Brahman jewel and seven gods before the global flood, and seven wiseacres were rescued from this flood. In Buddhism, Seven is the number of climbs and ascents to the topmost and access to the center. The seven steps of Buddha symbolize the ascent from seven floors of the universe and transcendental time and place. In ancient Egyptian tradition, the clothes of seven girls of Ra have seven knots. Seven bulls and seven cows are the symbol of fertility. Underground, There are seven houses and three seven-fold gates. Among Pythagoreans, seven, the cosmic number, consisting of three heavens and four earths, is also the symbol of perfection and the God of world lings.
“The Seven-fold division of a circle in the Islamic perspective is particularly associated with the seven heavens or planets and the seven days of the week. There are in addition other correspondences including the seven metals, etc. The seven-fold division gives rise to doubling to fourteen in a fortnight and the fourteen pure ones of the shiite branch of Islam: Muhammad, Fatimah, and the twelve Imams. Below these is the 28-day lunar cycle, which is also the basis of an emanation doctrine of creation developed by Ibn Arabi (Figure 19, Figure 20, Figure 21, Figure 22).
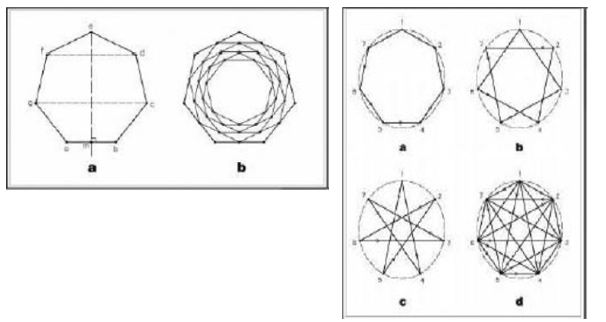
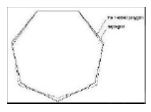
If a circle’s perimeter is divided into seven equal divisions, then the points of divisions respectively connected to each other, the result will be heptagon (Figure 23a). This shape is one of the regular polygons; therefore all its interior angles and all its sides are equal. The heptagon has seven apexes, seven sides, and seven symmetry axes that pass through each apex and the middle of its opposite side and are perpendicular to that side, and they also meet each other at the center (Figure 24a), em⊥ab, ab ‖ gc ‖ fd). The value of interior angles of the heptagon is 129° (Figure 25). If any point of a division is connected to its first, second, and third lateral point, the result will be, respectively, Figure 26a-c).
If all these points are connected to each other, i.e., each point is connected to the remaining six points, combinations of the three shapes mentioned will be achieved (Figure 26d).
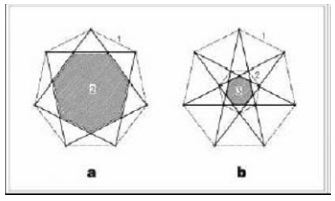
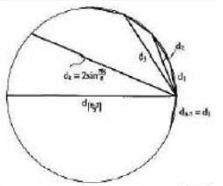
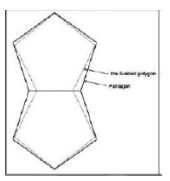
A heptagram has a direct relationship with a heptagon. If the sides of a heptagon are extended to meet each other, the seven-fold star will be produced (Figure 25). Also, there are three heptagons in the middle and around every seven-fold star (Figure 15b). If the middle of the sides of a heptagon are connected to each other, a smaller heptagon will emerge (Figure 27). If this action is continued, we will have a harmonic series of diminishing heptagons in a geometric form (Figure 24b). In the case of a heptagram, this is also valid. A method of drawing heptagon is shown in Figure 28. Proportions of diameters (interface lines between vertices) of polygons in general mode, and of pentagons and heptagons, respectively, are shown in Figure 28 and 29. Also, proportions of parts produced from the intersection of heptagon diameters is shown in Figure 30. Heptagon, heptagram, and the shapes produced from them, i.e. 14-sided polygon and 14 fold star, have also been frequently used in ornamental patterns and designs in architecture. In this section, some samples are given in Figure 20, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25.
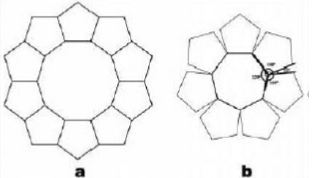
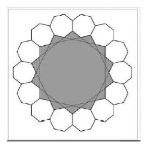
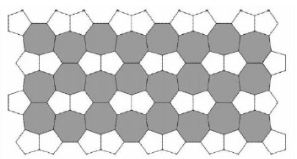
In geometric terms, both pentagon and heptagon, separately, cannot cover a two-dimensional surface without leaving gaps (Figure 31 and 32). Two compositions resulting from the combination of pentagons that can cover a two-dimensional surface are shown in Figure 33. But in a composition, both of these shapes cannot be regular. In Figure 33, the seven-sided polygons are regular but the remaining five-sided polygons are different from regular pentagons. In Figure 33, the five-sided are regular but the remaining seven-sided polygons are slightly different from regular heptagons. As was noted previously, the structure of a HC5C7 nanotube is a composition resulted from the combination of five-sided and seven-sided polygons that cover a two-dimensional surface without leaving gaps. This composition is shown in Figure 33a.
With knowing Relationship between structures of C5C7 Carbon Nanotubes and geometry of ornamental, it can be shown that human lifestyles are highly dependent and relevant in harmony with their natural internal structures. Also all of these symbols are in the religion of Islam and the remains of its architecture. In article mentioned in reference (from [3] until [6]), I prove that structures of C5C7, horizontally and vertically, are Constituent of order and constructor of unique rules in nature, carbon nanotubes and diamonds. Having the topological index of these forms and also their relationship with the geometric mathematics in it, can be achieved a new model for architecture, where is important strength and high impact strength for traditional and modern structures. Angles, lengths of edges, type of alignment of pentagons and seventh sides along and topological Indicators can define these patterns for us. Here, the most important issue is symmetry that is detailed in the article referred to [22]. In this article, I prove that carbon structures and symmetries in it, can cause the development of a system and its regular internal structure. Symmetry group in Algebra, Geological structure, C5C7 Carbon Nanotubes, Topological indices, geometry and recognition of the principles of modern and traditional architecture can load to the construction of solid structures.