Optimization of Physics-Mechanical Parameters of Hardening Complex Metal Coatings: Regression-Tensor Approach
A nonlinear multidimensional regression-tensor model is constructed and investigated to the end of grounding (necessary and sufficient conditions are implied) of an optimal multifactor physics-chemical process of hardening metal coatings. A robust-adaptive strategy of rational forming the goal functional of physics-mechanical quality of metal working is proposed. The results obtained may form a methodological ground in constructing the systems of computer-aided design, technologies of hardening surfaces of complex composite fabricated metal products of the basis of complex tribological tests.
Keywords: Tribological tests; Regression-Tensor Model; Hardening Metal Coatings
Development of methods of hardening the working surfaces of cutting machines presumes complex physics-chemical processes (PCP). So, essential still are the issues of formalization/processing the respective mathematical models. In the given context, regression models (linear ones, nonlinear ones, including matrix ones, where the important class of systems is represented by regression-tensor systems are in demand [1-7]. On the one hand, from the viewpoint of properties, these systems are quite close to polynomial ones, which presume a rather detailed analytical description on the basis of (i) tensor calculus, (ii) strong differentiability of vector mappings and (iii) the theory of extreme problems [2,7,8]. On the other hand, these systems acquire an important role in nonlinear modeling multifactor tribological properties of synthesized metal coatings, in particular, in prognostic description of surface nano-dimensional structures [9,10].
Below considered are the problems stated in the conclusions of paper, while the objective is not the formal precision conclusions but rather the clarity of the conceptions in development of tribological problems [5,11]. Hence the issue of forming the functional of metal coating physics-mechanical properties for the mode of hardening is solved in this context. Determined are the strong analytical interpretations of the interconnected conditions, which define an optimal mode of the PCP given by nonlinear constraints and providing for adequacy of the PCP model to the data of tribological tests [12,13]. So, solved is the problem of multicriterial identification (by the least squares method (LSM)) of coordinates of covariant tensors in the PCP equation as a multidimensional regression with a minimum tensor norm.
Let R be a field of real numbers, Rn be an n-dimensional vector space over R with the Euclidean norm ||.||Rn,
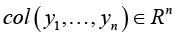
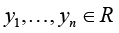
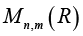
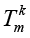
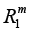
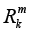
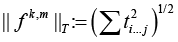
Let
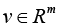
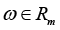
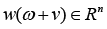
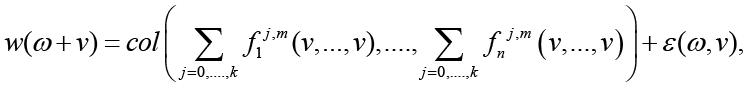
where
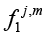
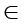
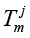
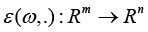
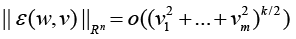
Where
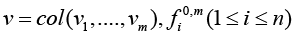
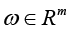
Remark 1: The description of PCP in terms of the regression system (1) is adequate on account of Proposition 2 related to continuous dependence of the solution of the PCP differential equation on the initial-boundary conditions and on the parameters [5,8,15].
The problem of an a posteriori regression-tensor modeling of an optimum PCP has been stated and investigated in detail in for a bivalent model (1). Furthermore, in the analytical solutions of three positions of the problem have been obtained [5]:
1) for a fixed index k, a given predictor
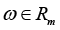
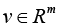
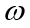
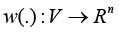
2) constructed is an algorithm of identification of coordinates of symmetric tensors
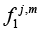
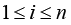
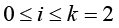
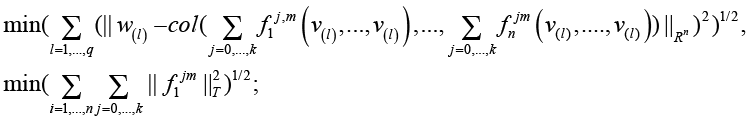
(2)
where
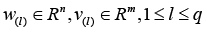
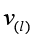
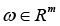
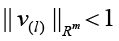
3) under the given predicting vector
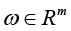
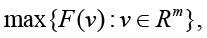
(3)
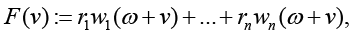
where vector function
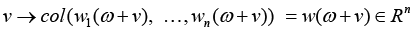
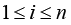
Problem statement (on the basis of the conclusion from) [5]. It is required to determine the necessary conditions in the solution of problem (3) when k = 3 (finding the stationary points in (3) for the 3-valent model (1)), and complement this determination with finding sufficient conditions of “v-optimization”, i.e. provision for the “elliptic character” of functional F critical points at the expense of dependence of spectral characteristics of its Hessian on variations of vector r := col
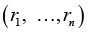
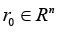
Consider the case of equations of multidimensional regression with the tensor structure of valence k = 3; solving problem (2) when k = 3 represents a trivial modification of the proof of Proposition 3 [5]. Under such a problem statement, the system of equations (1) may be represented in the vector-matrix-tensor form
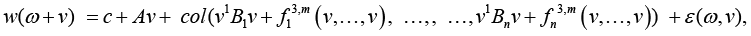
(4)
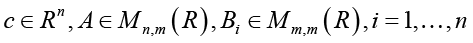
(in this case, we assume that each Bi is an upper triangular matrix), from now on, the upper prime index ` denotes the operation of transposition of either a vector or a matrix; the vector function ε(ω,.):
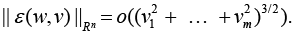
When k = 3, functional F is twice continuously differentiable, what guarantees the equality of mixed derivatives∂
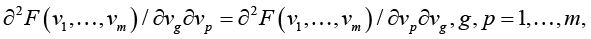
Proposition 1: Let
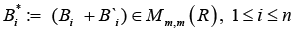
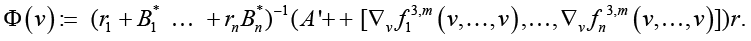
Hence the stationary points

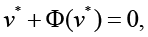
(5)
in this case, the sufficient condition of the statement that point v* of the space of predicting factors provides for “maximum quality of PCP” of the form
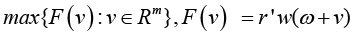
represents the following requirement: v* as a critical point of functional F(v) must be of special elliptic type. This is precisely the same as the statement that
det [bij]p < 0, p=1,…,m,
(6)
where
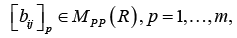
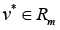
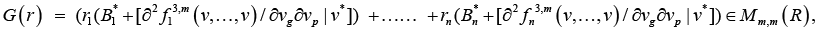
or similarly to state that the characteristic numbers λp of matrix G(r) satisfy the condition
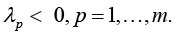
(7)
Corollary 1. When k = 2, Hessian G(r) of functional F is
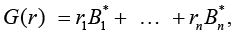
furthermore, when rank G(r) = m, the solution of equation (5) is unique and has the form
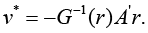
Obviously, (5) represents an intersection of m quadrics so, if conditions (6) (or, similarly, (7)) are not satisfied, then the critical point (/points) (5) is hyperbolic (saddle) one. Therefore, existence of a saddle point guaranteed by the replacement of < in (6) or (7) with > at least in one (not in all) inequalities (see e.g. (16) [5]). Replacement of inequality < with the reflexive < induces in v* the structure of stationary parabolic point of functional F(.); in this case, rank G(r)
It is clear that coordinate adjustment of vector r is one of the factors, which influence the geometry of F(.) at the critical point v*. This determines the statement of the problem of “adaptive correction”
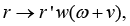
In this section we consider the following problem. It is necessary to use the regression-tensor model (4) as the basis and construct a numerical procedure of choosing the vector of weighting coefficients
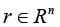
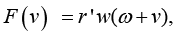
Remark 2: Despite the fact of algebraic equivalence (6)~(7), an attempt of usage of expansion of determinants (6) in constructing an adaptive correction
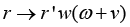
Necessary and sufficient conditions of solving problem (3) may be obtained only in exceptional cases. As a rule, for such problem statements, the general problem turms out to be NP-hard. Below, we intend to discuss an approach to solving this problem for the functional F(.). Such an approach is grounded on the provisions of the theory describing localizations and perturbations of eigenvalues of the matrix from [14]. Transformation of conditions (7) to the so called problem of quadratic stability represents another efficient technique. The problem of quadratic stability is usually reduced to constructing the Lyapunov function in the affine family of matrices under the assumption that this family, in turn, is functionally (due to the second formula in (3)) dependent on coordinates of vector
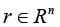
Let there be given an initial vector
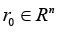
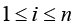
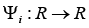
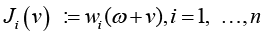
in the “auxiliary problems” related to forecasting PCP quality with respect to some indicators wi, 1 ≤ i ≤ n. Due to Corollary 2, for a bivalent model of regression (1) this situation is formalized in the following proposition [5].
Proposition 2: When k = 2, the initial weighting coefficient vector ()0010 , ,nrcolrr=… with the coordinates
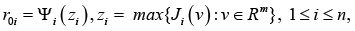
has the following analytical representation
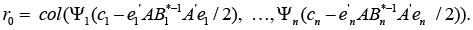
Remark 3: The statement “when k = 2” is not the key one because the given construction of vector r0 may be used also in the case of the 3-valent (with respect to the predictors) form of regression-tensor model (4); obviously, in this case, r0 may be “corrected”, on account of the condition of normalization
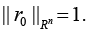
Next, denote by
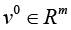
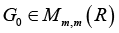
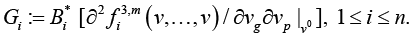
Hence, in case of varying of vector r according to the condition
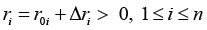

(8)
For any
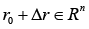
In case of an arbitrary matrix, the only description its eigenvalues presumes that these are solutions of its characteristic equation. Obtaining eigenvalues for the Hessian G(r) may also be (due to the Courant–Fischer Theorem, characterized as solving an optimization problem [14]. The sphere of possible interpretations of the Courant–Fischer Theorem includes the speculations of Weyl’s Theorem on the relations between the eigenvalues of Hessian G0 and any Hessian from the manifold
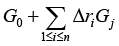
This allows one to understand the following “variation” sense of the robust-adaptive constructions needed for correction of
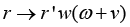
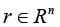
Proposition 3:
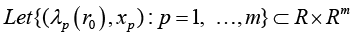
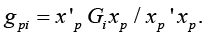
Hence the characteristic numbers
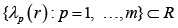
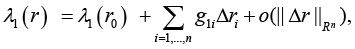
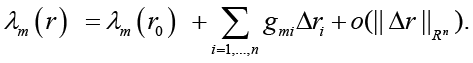
(9)
System (9) gives the possibility to assess how sensitive the eigennumbers of Hessians (8) to variations of the weighting coefficients
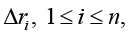
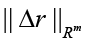
Corollary 2: If k = 2, n = m,
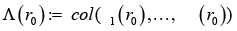
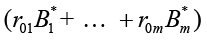
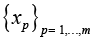
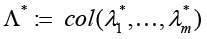
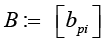
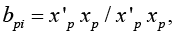
Then for
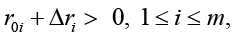
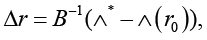
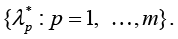
Remark 4: Since system (9) is valid for a small value of
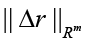
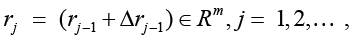
Constructed due to Corollaries 1, 2 on account that
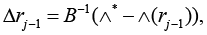
Converges, when the initial divergence
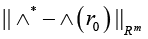
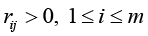
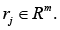
Now, while treating the situation in the context of Remark 4, consider the result of computing the upper estimate for the relative perturbation
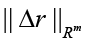
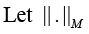
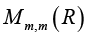
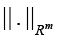
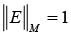
where
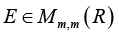
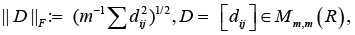
And the spectral (induced) matrix norm [20].
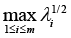
Thus, when turning back to Corollary 2, we have (due to the prototype of system (9)):
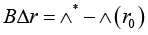
With det B ≠ 0. Suppose, vector
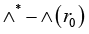
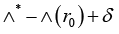
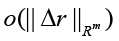
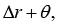
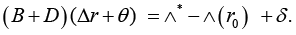
Obviously, vector
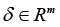
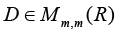
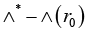
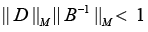
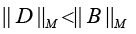
Details of the approach to computing the upper estimate of relative perturbation
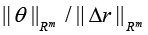
Corollary 3: Let (in addition to assumptions of Corollary 2)
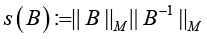
Be a conventional number of matrixes B, where ||.||M is the matrix norm equal to ||.||F or ||.||S. Hence the following analytical estimate is valid [20]
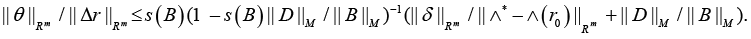
If
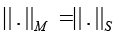
Remark 5: The construction of the spectral conventional number
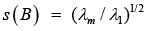
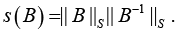
When the issues of mathematical modeling of complex physics-chemical objects and processes are discussed, the following technological procedure is normally implied: (i) natural differentiation between different aspects of a definitely given PCP (as an object of mathematical investigation), (ii) description of each of the aspects on the basis of one’s own (normally, comparatively narrow and easily observable) group of mathematical assumptions, (iii) subsequent integration of the partial results obtained on account of proper specification, (iv) turning back to consideration of the complex (integrated) functioning of PCP.
Within the frames of above paradigm, the idea of the present paper presumes to develop the results of and to point to natural relationship existing between the problem of defining the domain of the matrix Hessian function values at the critical point of its goal functional of physics-mechanical quality (3) for the process of hardening metal coating, expressed by equation (1) and by vector r of weighting coefficients in (3), which reflect the “priority” between
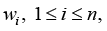
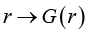
Eigen values of the matrix are definitely the roots of its characteristic polynomial, so, the result of Proposition 3 is, in essence, based on the assumption that eigen values (7) are continuously r-dependent on the elements of Hessian matrix G(r) in the process of the ongoing parametric correction of the goal functional F from (3). Noteworthy, some part of information turns out to be lost, when we deal only with the characteristic polynomial, because there are many different matrices with the given characteristic polynomial. So, no wonder that stronger results obtained in modeling the Hessian’s G(r) spectrum, in particular, Proposition 3 and Corollary 2, take account of the structure of matrix G(r); the latter assume some technical simplification, which follows from the assumption that any Hessian matrix is orthogonally similar to the real diagonal matrix [20].
Numerical methods of finding eigen values and eigen vectors represent one of the most important divisions of the general matrix theory. The present paper, considers analysis of vector
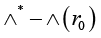
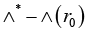
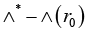
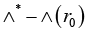
In conclusion, let us discuss another approach related to adaptive correction of
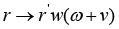
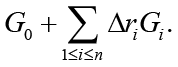
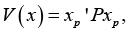
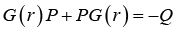
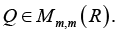
This work was supported by the Program “Leading Scientific Schools” (Project No. NSh-8081.2016.9) and by the Russian Foundation for Basic Research (Project No. 16-07-00201).



